Construct Binary Tree from given Parent Array representation

The problem “Construct Binary Tree from given Parent Array representation” states that you are given an array. This input array represents a binary tree. Now you need to construct a binary tree on the basis of this input array. The array stores the index of parent node at each index.

Example

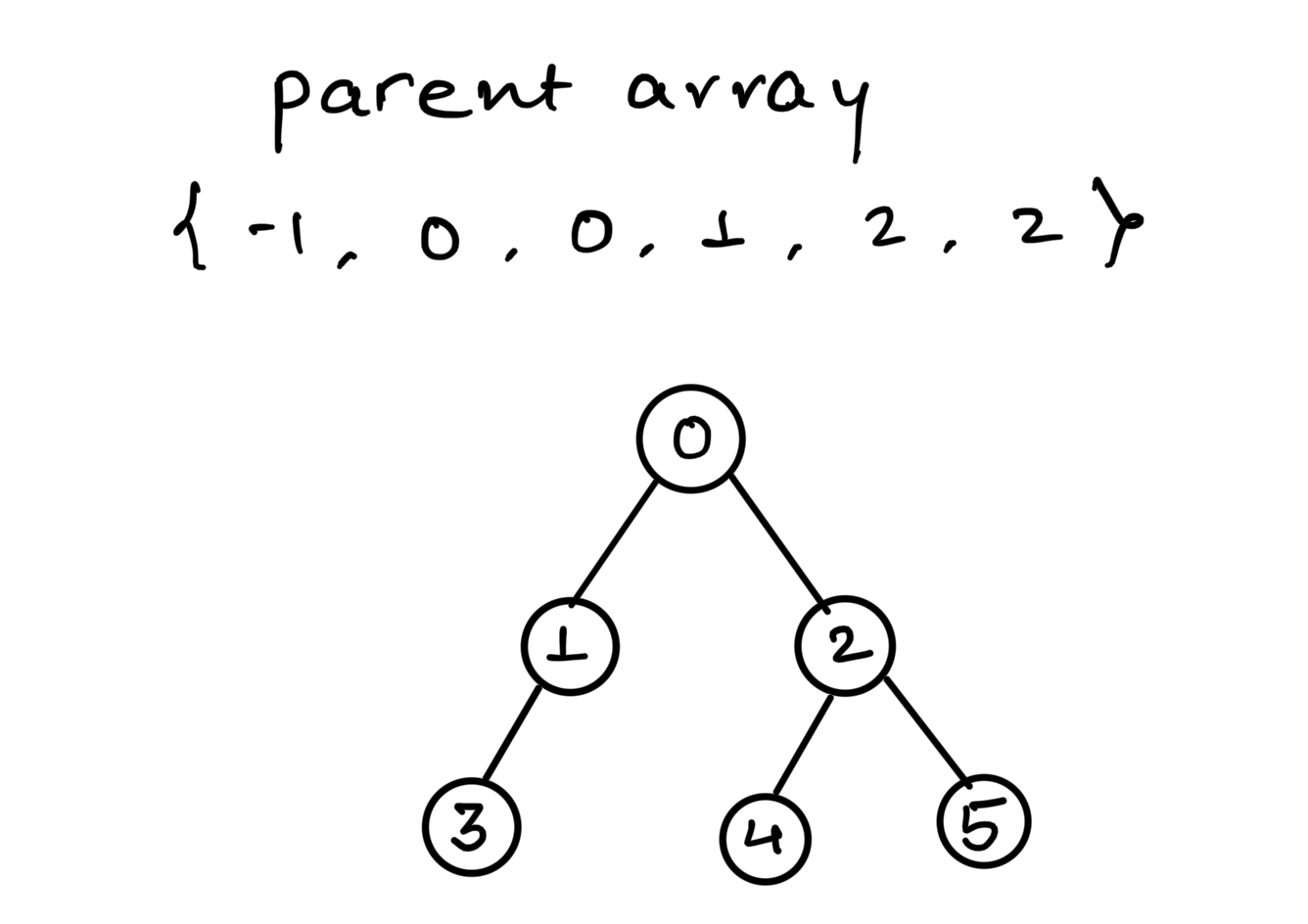
Inorder Traversal: 3 1 0 4 2 5

Approach

The problem asks us to construct binary tree from given parent array representation. A parent array stores the index of the parent node at each index of the array. Now you need to construct a binary tree using this array. The value -1 in the input array denotes the root node in the tree.

A naive approach is to keep on creating new nodes. When we create these nodes we always create the nodes in the order of their level in the binary tree. For example, first, we create root then its children, and so on. then as we create the nodes we attach the nodes in the tree with the help of pointers modification. But this approach is not efficient as we will be traversing the tree to find the parent of the currently created node.

A better and efficient solution is to keep track of the nodes which are already created. This way we don’t have to search for the parent of the current node. This solution is a bit different. Here we will first check if the parent node has been created. If it has been created then it’s fine. Otherwise, we recursively create all the parent nodes and then create the child node. This way we also keep on attaching the child nodes with the pointer modification.

Code

C++ code to Construct Binary Tree from given Parent Array representation

#include<bits/stdc++.h>
using namespace std;

struct node {
  int data;
  node *left, *right;
};

node* create(int data){
  node* tmp = new node();
  tmp->data = data;
  tmp->left = tmp->right = NULL;
  return tmp;
}

void inorder(node* root){
    if(root){
        inorder(root->left);
        cout<<root->data<<" ";
        inorder(root->right);
    }
}

void createNode(int a[], int i, node* created[]){
    // if current node is root
    if(a[i] == -1){
        node* cur = new node();
        cur->data = i;
        created[i] = cur;
        return;
    }

    // if the parent node has not been created
    if(created[a[i]] == NULL)
        createNode(a, a[i], created);

    // create current node
    node* cur = new node();
    cur->data = i;
    // insert the node value in created array
    created[i] = cur;

    // if left child of parent is null
    // attach current node as its left child
    if(created[a[i]]->left == NULL)
        created[a[i]]->left = cur;
    // else attach it as right child
    else if(created[a[i]]->right == NULL)
        created[a[i]]->right = cur;
}

int main()
{
  int a[] = {-1, 0, 0, 1, 2, 2};
  int n = (sizeof a) / (sizeof a[0]);
  node* created[n];
  memset(created, NULL, sizeof created);
  node* root = NULL;
  for(int i=0;i<n;i++){
        // if node has not been created
        if(created[i] == NULL)
            createNode(a, i, created);
        // store the root node
        if(a[i] == -1)
            root = created[i];
  }
  // print the inorder traversal of the root
  inorder(root);
}

3 1 0 4 2 5

Java code to Construct Binary Tree from given Parent Array representation

import java.util.*;

class node{
  int data;
  node left, right;
}

class Main{

  static node create(int data){
    node tmp = new node();
    tmp.data = data;
    tmp.left = tmp.right = null;
    return tmp;
  }

  static void inorder(node root){
      if(root != null){
          inorder(root.left);
          System.out.print(root.data+" ");
          inorder(root.right);
      }
  }

  static void createNode(int a[], int i, node created[]){
      // if current node is root
      if(a[i] == -1){
          node cur = new node();
          cur.data = i;
          created[i] = cur;
          return;
      }

      // if the parent node has not been created
      if(created[a[i]] == null)
          createNode(a, a[i], created);

      // create current node
      node cur = new node();
      cur.data = i;
      // insert the node value in created array
      created[i] = cur;

      // if left child of parent is null
      // attach current node as its left child
      if(created[a[i]].left == null)
          created[a[i]].left = cur;
      // else attach it as right child
      else if(created[a[i]].right == null)
          created[a[i]].right = cur;
  }

  public static void main(String[] args)
  {
    int a[] = {-1, 0, 0, 1, 2, 2};
    int n = 6;
    node created[] = new node[n];
    node root = null;
    for(int i=0;i<n;i++){
          // if node has not been created
          if(created[i] == null)
              createNode(a, i, created);
          // store the root node
          if(a[i] == -1)
              root = created[i];
    }
    // print the inorder traversal of the root
    inorder(root);
  }
}

3 1 0 4 2 5

Complexity Analysis

Time Complexity

O(N), because even though we are using recursion. If the node is created we never create the same node again. Thus the time limit is linear.

Space Complexity

O(N), because we created an array of nodes to check if the node has been created or not. Thus the space complexity is also linear.