Table of Contents
Problem Statement
“Convert BST into a Min-Heap without using array” problem states that you are given a BST (binary search tree) and you need to convert it into a min-heap. The min-heap should contain all the elements in the binary search tree. The algorithm should run in linear time complexity.
Example
Input
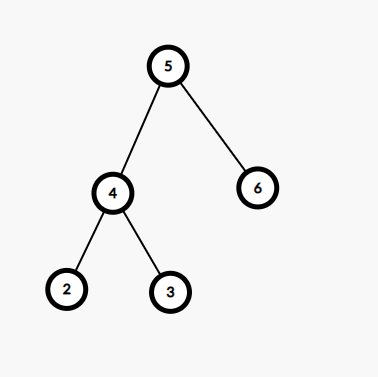
Output
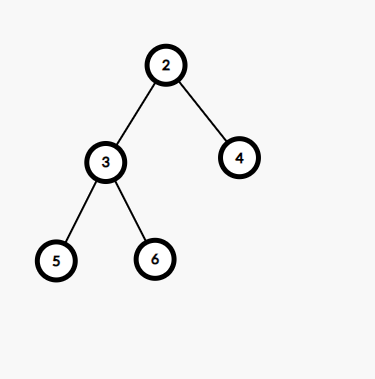
Approach to Convert BST into a Min-Heap without using array
Naive Approach
“Convert BST into a Min-Heap without using array” problem can be solved if we first store the in-order traversal of the binary search tree. And after finding the in-order traversal, we start creating min-heap ( complete binary tree having all children in subtree lesser than the parent ). So, how will we create the min-heap? We will create the min-heap by level placing the elements in level order traversal that will ensure the complete binary tree property. And since we have in-order traversal we are sure that property of min-heap is satisfied (parent is smaller than both of its children). But this requires storing in-order traversal.
Efficient Approach
We can solve this problem in O(1) space if we first convert our binary search tree into a linked list. There is a condition on the linked list as well that it must be in sorted order. For doing that, we first traverse the right subtree and then traverse the left subtree. Because we insert the nodes in the linked list at the start of it. This way, we are ensuring that the linked list remains sorted. Once, we have our sorted linked list. We rearrange the nodes’ left and right pointers such that our complete binary tree property is satisfied. As we were doing in the naive approach, we used level order traversal for creating min-heap. Here also we will use the same.
Code
C++ code to Convert BST into a Min-Heap without using array
#include <bits/stdc++.h>
using namespace std;
struct node{
int data;
node* left;
node* right;
};
node* create(int data){
node* tmp = new node();
tmp->data = data;
tmp->left = tmp->right = NULL;
return tmp;
}
// prints the level order traversal of the tree
void levelOrderTraversal(node *root)
{
if (root == NULL) return;
queue<node*> q;
q.push(root);
while(!q.empty()){
int qSize = q.size();
while(qSize--){
node* nodeAtFront = q.front();
q.pop();
if(nodeAtFront->left)
q.push(nodeAtFront->left);
if(nodeAtFront->right)
q.push(nodeAtFront->right);
cout<<nodeAtFront->data<<" ";
}
cout<<endl;
}
}
void convertBSTToLinkedList(node* root, node* &head_ref)
{
if(!root)
return;
//first convert right subtree into linked list
convertBSTToLinkedList(root->right, head_ref);
// insert root into the linked list
root->right = head_ref;
//if head pointer exists, then point left pointer to NULL
if(head_ref)
head_ref->left = NULL;
// now head of linked list is current root
head_ref = root;
// convert left subtrree recursively
convertBSTToLinkedList(root->left, head_ref);
}
void convertLinkedListToMinHeap(node* &root, node* head)
{
// Base Case
if(!head)
return;
//traverse over the linked list in level order traversal fashion
queue<node*> q;
//first node of min heap will be smallest element
//i.e. first element of inorder traversal
root = head;
// point head to next node
head = head->right;
// left is already null
root->right = NULL;
// insert into queue
q.push(root);
while(head)
{
node* nodeAtFront = q.front();
q.pop();
// now remove one node from linked list and make left child
// if there are more nodes make a right child
// push them into queue
node* leftNode = head;
head = head->right;
leftNode->right = NULL;
nodeAtFront->left = leftNode;
q.push(leftNode);
// similarly do the same for right child if it exists
if(head){
node* rightNode = head;
head = head->right;
rightNode->right = NULL;
nodeAtFront->right = rightNode;
q.push(rightNode);
}
}
}
// Function to convert BST into a Min-Heap
// without using any extra space
node* BSTToMinHeap(node* &root)
{
// head of Linked List
node *head = NULL;
// get converted linked list
convertBSTToLinkedList(root, head);
// now set the root for min heap
root = NULL;
// convert the linked list into min heap
convertLinkedListToMinHeap(root, head);
}
int main()
{
node* root = create(5);
root->left = create(4);
root->right = create(6);
root->left->left = create(2);
root->left->right = create(3);
BSTToMinHeap(root);
levelOrderTraversal(root);
return 0;
}
2 4 3 5 6
Java code to Convert BST into a Min-Heap without using array
import java.util.*;
import java.lang.*;
import java.io.*;
class node{
int data;
node left;
node right;
}
class Tree{
static node root;
static node create(int data){
node tmp = new node();
tmp.data = data;
tmp.left = null;
tmp.right = null;
return tmp;
}
static void levelOrderTraversal(node root)
{
if (root == null) return;
Queue<node> q = new LinkedList<>();
q.add(root);
while(!q.isEmpty()){
int qSize = q.size();
while(qSize-- > 0){
node nodeAtFront = q.peek();
q.remove();
if(nodeAtFront.left != null)
q.add(nodeAtFront.left);
if(nodeAtFront.right != null)
q.add(nodeAtFront.right);
System.out.print(nodeAtFront.data+" ");
}
System.out.println();
}
}
static node convertBSTToLinkedList(node root, node head_ref)
{
if(root == null)
return head_ref;
//first convert right subtree into linked list
head_ref = convertBSTToLinkedList(root.right, head_ref);
// insert root into the linked list
root.right = head_ref;
//if head pointer exists, then point left pointer to NULL
if(head_ref != null)
head_ref.left = null;
// now head of linked list is current root
head_ref = root;
// convert left subtrree recursively
head_ref = convertBSTToLinkedList(root.left, head_ref);
return head_ref;
}
static node convertLinkedListToMinHeap(node root, node head)
{
// Base Case
if(head == null)
return null;
//traverse over the linked list in level order traversal fashion
Queue<node> q = new LinkedList<>();
//first node of min heap will be smallest element
//i.e. first element of inorder traversal
root = head;
// point head to next node
head = head.right;
// left is already null
root.right = null;
// insert into queue
q.add(root);
while(head != null)
{
node nodeAtFront = q.peek();
q.remove();
// now remove one node from linked list and make left child
// if there are more nodes make a right child
// push them into queue
node leftNode = head;
head = head.right;
leftNode.right = null;
nodeAtFront.left = leftNode;
q.add(leftNode);
// similarly do the same for right child if it exists
if(head != null){
node rightNode = head;
head = head.right;
rightNode.right = null;
nodeAtFront.right = rightNode;
q.add(rightNode);
}
}
return root;
}
// Function to convert BST into a Min-Heap
// without using any extra space
static node BSTToMinHeap(node root)
{
// head of Linked List
node head = null;
// get converted linked list
head = convertBSTToLinkedList(root, head);
// now set the root for min heap
root = null;
// convert the linked list into min heap
root = convertLinkedListToMinHeap(root, head);
return root;
}
public static void main(String[] args)
{
node root = create(5);
root.left = create(4);
root.right = create(6);
root.left.left = create(2);
root.left.right = create(3);
root = BSTToMinHeap(root);
levelOrderTraversal(root);
}
}2 4 3 5 6
Complexity Analysis
Time Complexity
O(N), because we have first converted the tree into a linked list and then id a level order traversal. Both pf which are liner time complexity operation. Thus a linear time complexity is achieved.
Space Complexity
O(log N), because we have used a queue to store the children in a single level. This takes logarithmic space complexity. But the algorithm itself works in place.