Table of Contents
Problem
Given a linked list. The elements of the linked list are in increasing order. Convert the given linked list into a highly balanced binary search tree.
A highly balanced binary search tree is a binary search tree in which the difference between the depth of two subtrees of any node is at most one.
Example
Input
1->2->3->4->5->6->7
Output
4 2 6 1 3 5 7
Explanation
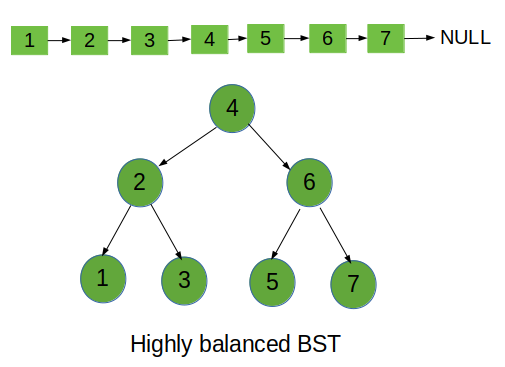
The given linked list is converted to a highly balanced binary search tree. As in the given binary tree, the elements smaller than the root element are to the left of the root and the elements greater than the root element is to the right of the root, So the given tree is a binary search tree. Also, the difference between the depth of two subtrees of any node is 0 for all the nodes so this binary search tree is a highly balanced binary search tree.
Approach for Convert Sorted List to Binary Search Tree
We will use a trick to form a balanced binary search tree from the given linked list. In place of start creating a tree from the root, we will start creating a tree from the leaf.
- We count the number of elements in the linked list.
- Here first n/2 elements will form left subtree then one element will form the root and remaining elements will form the right subtree.
- Using recursion we recursively construct the left subtree.
- We create a root node.
- Link the left subtree with the root node.
- We will recursively construct the right subtree from the remaining elements.
- Link the right subtree with the root node.
- While creating the tree we also keep increasing the pointer of the liked list to point to the next element each time.
Implementation for Convert Sorted List to Binary Search Tree
C++ code for Convert Sorted List to Binary Search Tree
// C++ implementation of above approach
#include <bits/stdc++.h>
using namespace std;
/* Link list node */
class LNode
{
public:
int data;
LNode* next;
};
/* A Binary Tree node */
class TNode
{
public:
int data;
TNode* left;
TNode* right;
};
TNode* newNode(int data);
int countLNodes(LNode *head);
TNode* sortedListToBSTRecur(LNode **head_ref, int n);
/* This function counts the number of
nodes in Linked List and then calls
sortedListToBSTRecur() to construct BST */
TNode* sortedListToBST(LNode *head)
{
/*Count the number of nodes in Linked List */
int n = countLNodes(head);
/* Construct BST */
return sortedListToBSTRecur(&head, n);
}
TNode* sortedListToBSTRecur(LNode **head_ref, int n)
{
/* Base Case */
if (n <= 0)
return NULL;
/* Recursively construct the left subtree */
TNode *left = sortedListToBSTRecur(head_ref, n/2);
TNode *root = newNode((*head_ref)->data);
root->left = left;
*head_ref = (*head_ref)->next;
/* Recursively construct the right
subtree and link it with root
The number of nodes in right subtree
is total nodes - nodes in
left subtree - 1 (for root) which is n-n/2-1*/
root->right = sortedListToBSTRecur(head_ref, n - n / 2 - 1);
return root;
}
/* UTILITY FUNCTIONS */
/* A utility function that returns
count of nodes in a given Linked List */
int countLNodes(LNode *head)
{
int count = 0;
LNode *temp = head;
while(temp)
{
temp = temp->next;
count++;
}
return count;
}
void push(LNode** head_ref, int new_data)
{
/* allocate node */
LNode* new_node = new LNode();
/* put in the data */
new_node->data = new_data;
/* link the old list off the new node */
new_node->next = (*head_ref);
/* move the head to point to the new node */
(*head_ref) = new_node;
}
void printList(LNode *node)
{
while(node!=NULL)
{
cout << node->data << " ";
node = node->next;
}
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
TNode* newNode(int data)
{
TNode* node = new TNode();
node->data = data;
node->left = NULL;
node->right = NULL;
return node;
}
void preOrder(TNode* node)
{
if (node == NULL)
return;
cout<<node->data<<" ";
preOrder(node->left);
preOrder(node->right);
}
/* Driver code*/
int main()
{
/* Start with the empty list */
LNode* head = NULL;
/* Let us create a sorted linked list to test the functions
Created linked list will be 1->2->3->4->5->6->7 */
push(&head, 7);
push(&head, 6);
push(&head, 5);
push(&head, 4);
push(&head, 3);
push(&head, 2);
push(&head, 1);
cout<<"Given Linked List ";
printList(head);
/* Convert List to BST */
TNode *root = sortedListToBST(head);
cout<<"\nPreOrder Traversal of constructed BST ";
preOrder(root);
return 0;
}Given Linked List 1 2 3 4 5 6 7 PreOrder Traversal of constructed BST 4 2 1 3 6 5 7
Java code for Convert Sorted List to Binary Search Tree
class LinkedList {
/* head node of link list */
static LNode head;
/* Link list Node */
class LNode
{
int data;
LNode next, prev;
LNode(int d)
{
data = d;
next = prev = null;
}
}
/* A Binary Tree Node */
class TNode
{
int data;
TNode left, right;
TNode(int d)
{
data = d;
left = right = null;
}
}
TNode sortedListToBST()
{
/*Count the number of nodes in Linked List */
int n = countNodes(head);
/* Construct BST */
return sortedListToBSTRecur(n);
}
TNode sortedListToBSTRecur(int n)
{
/* Base Case */
if (n <= 0)
return null;
/* Recursively construct the left subtree */
TNode left = sortedListToBSTRecur(n / 2);
TNode root = new TNode(head.data);
// Set pointer to left subtree
root.left = left;
head = head.next;
root.right = sortedListToBSTRecur(n - n / 2 - 1);
return root;
}
/* UTILITY FUNCTIONS */
/* A utility function that returns count of nodes in a
given Linked List */
int countNodes(LNode head)
{
int count = 0;
LNode temp = head;
while (temp != null)
{
temp = temp.next;
count++;
}
return count;
}
void push(int new_data)
{
/* allocate node */
LNode new_node = new LNode(new_data);
/* since we are adding at the begining,
prev is always NULL */
new_node.prev = null;
/* link the old list off the new node */
new_node.next = head;
/* change prev of head node to new node */
if (head != null)
head.prev = new_node;
/* move the head to point to the new node */
head = new_node;
}
void printList(LNode node)
{
while (node != null)
{
System.out.print(node.data + " ");
node = node.next;
}
}
void preOrder(TNode node)
{
if (node == null)
return;
System.out.print(node.data + " ");
preOrder(node.left);
preOrder(node.right);
}
public static void main(String[] args) {
LinkedList llist = new LinkedList();
llist.push(7);
llist.push(6);
llist.push(5);
llist.push(4);
llist.push(3);
llist.push(2);
llist.push(1);
System.out.println("Given Linked List ");
llist.printList(head);
/* Convert List to BST */
TNode root = llist.sortedListToBST();
System.out.println("");
System.out.println("Pre-Order Traversal of constructed BST ");
llist.preOrder(root);
}
}Given Linked List 1 2 3 4 5 6 7 PreOrder Traversal of constructed BST 4 2 1 3 6 5 7
Time complexity
O(n) because we are traversing the linked list only once.
Space complexity
O(n) because we are creating a tree of n nodes.