Diagonal Traversal of Binary Tree

Problem Statement

The problem “Diagonal Traversal of Binary Tree” states that you are given a binary tree and now you need to find the diagonal view for the given tree. When we see a tree from the top-right direction. The nodes which are visible to us is the diagonal view of the binary tree.

Example

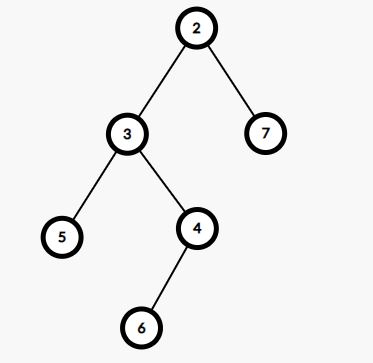
2 7
3 4
5 6

Explanation

The first diagonal has nodes 2, 7 in there. Then the second diagonal has 3, 4, similarly for the third diagonal 5, 6. Thus the output has printed in a way such that the elements from the same diagonal have in the same line.

Approach

The problem asks us to print the nodes which are visible to us from the top-right direction. So how do we solve the problem?

We will do an inorder traversal of the binary tree. While doing this, we will keep track of the distance in a diagonal direction. Whenever we move in the left direction we add 1 to the diagonal distance and if we moved in the right direction we don’t add any value to the distance. So, while doing this we will keep track of the nodes visited in a map. We will create a map with diagonal distance as key and a vector as value. because we will add the nodes with diagonal distance in a vector. And as we would have traversed through the whole tree. After the traversal, we would have kept the nodes in the vectors as per their diagonal distance.

After all of these calculations, simply print the elements in the map while separating the nodes from each of the vectors.

C++ code to print Diagonal Traversal of Binary Tree

#include <bits/stdc++.h>
using namespace std;

struct node{
    int data;
    node *left, *right;
};

node* create(int data){
    node* tmp = new node();
    tmp->data = data;
    tmp->left = tmp->right = NULL;
    return tmp;
}

void diagonalView(node* root, int dis, map<int, vector<int>> &m){
    if(root){
        m[dis].push_back(root->data);
        // move in the left direction with dis+1 distance
        diagonalView(root->left, dis+1, m);
        // move in the right direction with dis distance
        diagonalView(root->right, dis, m);
    }
}

int main(){
    node *root = create(2);
    root->left = create(3);
    root->right = create(7);
    root->left->left = create(5);
    root->left->right = create(4);
    root->left->right->left = create(6);

    map<int, vector<int>> m;
    diagonalView(root, 0, m);
    for(auto x: m){
        for(auto nodes: x.second)
            cout<<nodes<<" ";
        cout<<endl;
    }
}

2 7
3 4
5 6

Java code to print Diagonal Traversal of Binary Tree

import java.util.*;

class node{
  int data;
  node left, right;
}

class Main{

  static node create(int data){
      node tmp = new node();
      tmp.data = data;
      tmp.left = tmp.right = null;
      return tmp;
  }

  static void diagonalView(node root, int dis, Map<Integer, Vector<Integer>> m){
      if(root != null){
      	Vector<Integer> v = m.get(dis);
      	if(v == null){
      		v = new Vector<Integer>();
      		v.add(root.data);
      	}
      	else
      		v.add(root.data);
          m.put(dis, v);
          // move in the left direction with dis+1 distance
          diagonalView(root.left, dis+1, m);
          // move in the right direction with dis distance
          diagonalView(root.right, dis, m);
      }
  }

  public static void main(String[] args){
    node root = create(2);
      root.left = create(3);
      root.right = create(7);
      root.left.left = create(5);
      root.left.right = create(4);
      root.left.right.left = create(6);

      Map<Integer, Vector<Integer>> m = new TreeMap<Integer, Vector<Integer>>();
      diagonalView(root, 0, m);
      for(Map.Entry<Integer, Vector<Integer>> entry : m.entrySet())
          System.out.println(entry.getValue());
  }
}

[2, 7]
[3, 4]
[5, 6]

Complexity Analysis

Time Complexity

O(NlogN), because we have traversed the tree and have updated the values. Because we have used a map, insertion, deletion, and searching is done in O(logN) time.

Space Complexity

O(N), because we are storing all the nodes in the map. The space complexity is linear.