The problem “Given a binary tree, how do you remove all the half nodes?” states that you are given a binary tree. Now you need to remove the half nodes. A half node is defined as a node in the tree that has only a single child. Either it is left child or right child.
Table of Contents
Example
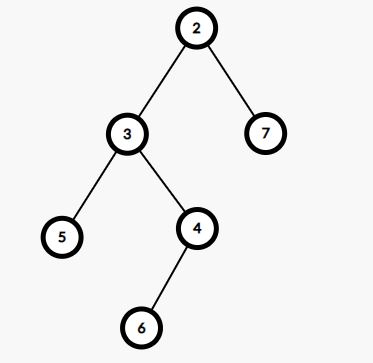
Inorder Traversal of tree after half nodes removal: 5 3 6 2 7
Explanation
The node with value 4 has a single left child. Thus it has been removed from the binary tree and its left child has moved up the tree. Because there is only one-half node. After its removal, we are left with a tree whose inorder traversal has been printed as output.
Approach
The problem has given a binary tree, how do you remove all the half nodes? Before jumping right into the solution. We should first know what is a half node? A half node is a node in the binary tree that has a single child. Thus a node with either no child or two children is not considered as a half node. Since now we know what is a half node. We should move ahead with the solution to the problem. The solution is simple. We simply traverse the tree and whenever we find a half node we replace it with its child. We check if the left child exists and the right child is null. Then we replace the parent(or half node) with its left child. Similarly, if the right child is the only child. The right child replaces the parent node.
Code
C++ code to remove all the half nodes
#include<bits/stdc++.h>
using namespace std;
struct node {
int data;
node *left, *right;
};
node* create(int data){
node* tmp = new node();
tmp->data = data;
tmp->left = tmp->right = NULL;
return tmp;
}
node* removeHalfNode(node* &root){
if(!root)
return NULL;
if(root->left == NULL && root->right != NULL)
root = removeHalfNode(root->right);
else if(root->left != NULL && root->right == NULL)
root = removeHalfNode(root->left);
else {
removeHalfNode(root->left);
removeHalfNode(root->right);
}
return root;
}
void inorder(node* root){
if(root){
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
}
}
int main()
{
node* root = create(5);
root->left = create(7);
root->right = create(3);
root->left->left = create(9);
root->left->right = create(6);
root->left->right->left = create(1);
cout<<"Inorder traversal before removing the half nodes"<<endl;
inorder(root);
cout<<endl<<"Inorder traversal after removing the half nodes"<<endl;
root = removeHalfNode(root);
inorder(root);
}
Inorder traversal before removing the half nodes 9 7 1 6 5 3 Inorder traversal after removing the half nodes 9 7 1 5 3
Java code to remove all the half nodes
import java.util.*;
class node{
int data;
node left, right;
}
class Main{
static node create(int data){
node tmp = new node();
tmp.data = data;
tmp.left = tmp.right = null;
return tmp;
}
static node removeHalfNode(node root){
if(root == null)
return null;
root.left = removeHalfNode(root.left);
root.right = removeHalfNode(root.right);
if(root.left == null && root.right == null)
return root;
if(root.left == null){
node Node = root.right;
return Node;
}
if(root.right == null){
node Node = root.left;
return Node;
}
return root;
}
static void inorder(node root){
if(root != null){
inorder(root.left);
System.out.print(root.data+" ");
inorder(root.right);
}
}
public static void main(String[] args)
{
node root = create(5);
root.left = create(7);
root.right = create(3);
root.left.left = create(9);
root.left.right = create(6);
root.left.right.left = create(1);
System.out.println("Inorder traversal before removing the half nodes");
inorder(root);
System.out.println("\nInorder traversal after removing the half nodes");
root = removeHalfNode(root);
inorder(root);
}
}Inorder traversal before removing the half nodes 9 7 1 6 5 3 Inorder traversal after removing the half nodes 9 7 1 5 3
Complexity Analysis
Time Complexity
O(N), because we have traversed over all the nodes in the binary tree. The time complexity is linear.
Space Complexity
O(H), the algorithm is a recursive algorithm. Thus the space complexity is dependent on the compiler stack which in turn is dependent on the height of the tree.