Insertion in a Binary Tree

In this article, we will learn the insertion in a binary tree. We have already seen the concept of BFS in the previous article, so here we will use the same concept to insert the data in a binary tree. The concept is traversing the tree in level order and if we encounter a node whose left or right or both nodes are NULL then insert the data at the position of the NULL node (preference first from left). See the below example for more understanding.

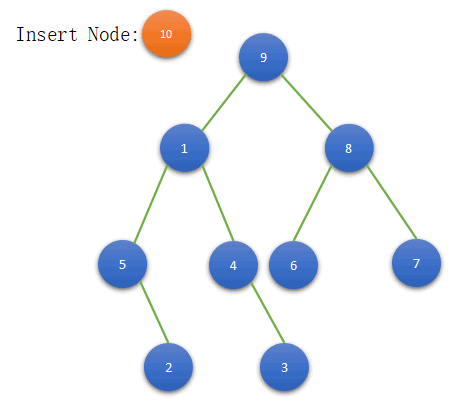
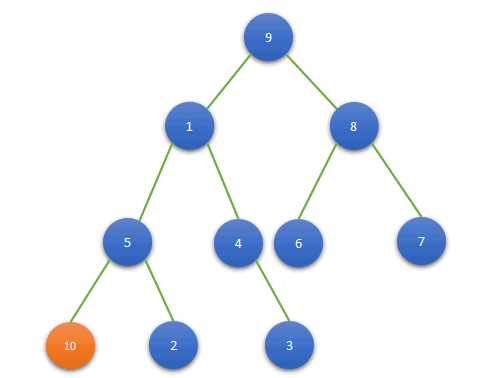
We want to insert a node with data(10) in the above binary tree. When we use BFS then we find a node(5) having left child NULL. So, we add a node with data(10) as the left child of 5.

C++ Code for Insertion in a Binary Tree

/*C++ Implementation of Insertion in Binary Tree*/ 
#include<bits/stdc++.h> 
using namespace std; 
/*Structure of Node of BT which contain pointer to left child and right child and a data for node.*/
struct Node{
    int data;
    struct Node* left;// for left child;
    struct Node* right;// for right child;
    Node(int value)// create a node using new_Node;
    {
        data=value;
        left=NULL;
        right=NULL;
    }
};
/*Function which print bfs of the given tree*/ 
void level_order(Node* root)
{
   if(root==NULL)
   { 
       return;
   }
   queue<Node*> q;
   q.push(root);
   while(!q.empty())
   {
       Node* temp=q.front();
       cout<<temp->data<<" ";
       q.pop();
       if(temp->left!=NULL)
       {
           q.push(temp->left);
       }
       if(temp->right!=NULL)
       {
           q.push(temp->right);
       }
   }
   cout<<endl;
}
void add(Node* root,int value)
{
    queue<Node*> q;
    q.push(root);
    while(!q.empty())
    {
        Node* temp=q.front();
        q.pop();
        if(temp->left==NULL)
        {
            temp->left=new Node(value);
            goto label;
        }
        if(temp->right==NULL)
        {
            temp->right=new Node(value);
            goto label;
        }
        if(temp->left!=NULL)
        {
           q.push(temp->left); 
        }
        if(temp->right!=NULL)
        {
            q.push(temp->right);
        }
    }
    label:;
}
int main() 
{ 
    /*construct tree*/
    Node* root= new Node(9);
    root->left= new Node(1);
    root->right= new Node(8);
    root->left->left= new Node(5);
    root->left->right= new Node(4);
    root->right->left= new Node(6);
    root->right->right= new Node(7);
    root->left->left->right= new Node(2);
    root->left->right->right= new Node(3);
    int value;
    cin>>value;//input the data of node which we want to insert;
    cout<<"Level order traversal before Insertion of node: ";
    level_order(root);
    /*add the node*/
    add(root, value);
    cout<<"Level order traversal after Insertion of node: ";
    level_order(root);
    return 0; 
}

Output:
Level order traversal before Insertion of node: 9 1 8 5 4 6 7 2 3 
Level order traversal after Insertion of node: 9 1 8 5 4 6 7 10 2 3

Time complexity of Insertion in a Binary Tree

O(N) where N is the number of nodes in the given binary tree. The worst-case of time complexity occur when every node has exactly one child. Here we visit in linear time. Linear time complexity means it’s in order of N.

Space Complexity

O(1) because we don’t create any space to add the node in the given binary tree.

Reference Interview Question