Iterative Preorder Traversal

The problem “Iterative Preorder Traversal” states that you are given a binary tree and now you need to find the preorder traversal of the tree. We are required to find the preorder traversal using iterative method and not the recursive approach.

Example

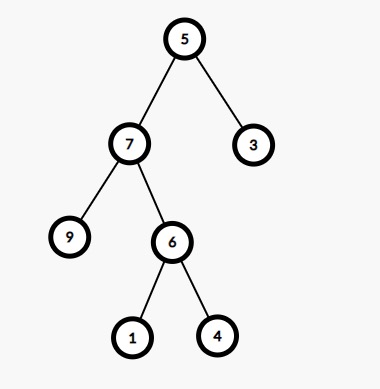
5 7 9 6 1 4 3

Approach to print

The problem statement asks us to print the preorder traversal of the given binary tree using the iterative method. Generally, we use the recursive method because that is easier. But sometimes it is asked to solve the problem using iteration. Thus we are required here to perform an iterative preorder traversal of the tree.

Previously we were using recursion to print the traversal. So to replace the recursion, we have to use a stack data structure. So we will be using a stack data structure to store the nodes which will be required afterward. In preorder traversal first, we print the root then recursively print the left subtree, and in the end, recursively print the right subtree. Here in this algorithm we will run a loop that will run until our current node is not null. And then we will keep on storing the right child in stack if the right child exists. Then we move to the left child. If the left child is null, we remove the elements from the stack and assign them as current node. This way in the end we would have traversed the tree in preorder manner.

Code

C++ code to print Iterative Preorder Traversal

#include<bits/stdc++.h>
using namespace std;

struct node {
  int data;
  node *left, *right;
};

node* create(int data){
  node* tmp = new node();
  tmp->data = data;
  tmp->left = tmp->right = NULL;
  return tmp;
}

void preorder(node* root){
    // create a stack
    stack<node*> s;

    while(root){
        // print the current node
        cout<<root->data<<" ";
        
        // if current node has right sub-tree
        // then store it and use it afterwards
        if(root->right)
            s.push(root->right);
        // now move to left child of current node
        // if the left child does not exists 
        // then in the next condition we will move up in the tree
        // and assign the right children which 
        // we have been storing the stack
        root = root->left;
        if(!root && !s.empty()){
                root = s.top(), s.pop();
        }
    }
}

int main()
{
  node* root = create(5);
  root->left = create(7);
  root->right = create(3);
  root->left->left = create(9);
  root->left->right = create(6);
  root->left->right->left = create(1);
  root->left->right->right = create(4);

  preorder(root);
}

5 7 9 6 1 4 3

Java code to print Iterative Preorder Traversal

import java.util.*;

class node{
  int data;
  node left, right;
}

class Main{

  static node create(int data){
    node tmp = new node();
    tmp.data = data;
    tmp.left = tmp.right = null;
    return tmp;
  }

  static void preorder(node root){
      // create a stack
      Stack<node> s = new Stack<node>();

      while(root != null){
          // print the current node
          System.out.print(root.data+" ");

          // if current node has right sub-tree
          // then store it and use it afterwards
          if(root.right != null)
              s.add(root.right);
          // now move to left child of current node
          // if the left child does not exists
          // then in the next condition we will move up in the tree
          // and assign the right children which
          // we have been storing the stack
          root = root.left;
          if(root == null && !s.empty()){
                  root = s.peek();
                  s.pop();
          }
      }
  }

  public static void main(String[] args)
  {
    node root = create(5);
    root.left = create(7);
    root.right = create(3);
    root.left.left = create(9);
    root.left.right = create(6);
    root.left.right.left = create(1);
    root.left.right.right = create(4);

    preorder(root);
  }
}

5 7 9 6 1 4 3

Complexity Analysis

Time Complexity

O(N), since we have traversed all the elements of the tree. Thus the time complexity is linear.

Space Complexity

O(H), in the worst-case each of the nodes can have the right child. Because we are storing the right child of each node in the path to the left child. Thus we can store at max O(H) nodes in the stack.