Kth ancestor of a node in binary tree

Problem Statement

The problem “Kth ancestor of a node in binary tree” states that you are given a binary tree and a node. Now we need to find the kth ancestor of this node. An ancestor of any node is the nodes that lie on the path from the root to the parent of the node.

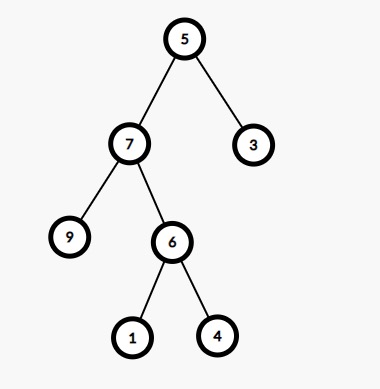
Example

2nd ancestor of 4 is 7

Approach

The problem asks to print the kth ancestor of a given node. An ancestor is nothing but the nodes which come in the path of the node from the root. The parent of a node is also its ancestor.

A simple and easy solution is to use BFS. This solution is easy and efficient also but requires us to first store the parent of each node in the tree. Then the problem simply boils down to moving up in the tree k distance. So instead of pushing the children of the nodes. We will only push the parent of each node.

But in this solution, instead of going with the approach discussed above. we will use a DFS based approach. In the DFS based approach, we are taking advantage of backtracking. Once we find the node in the tree, the recursion keeps moving back to the function which called this recursive function. So when we move k steps back, we print the node at the level. Because that is our kth ancestor and return null.

The same approach is used in the inorder successor of the binary tree.

Code

C++ code to find Kth ancestor of a node in binary tree

#include<bits/stdc++.h>
using namespace std;

struct node {
  int data;
  node *left, *right;
};

node* create(int data){
  node* tmp = new node();
  tmp->data = data;
  tmp->left = tmp->right = NULL;
  return tmp;
}

node* tmp = NULL;

node* kthAncestor(node *root, int cur, int &k)
{
  if (root == NULL)
    return NULL;
  if (root->data == cur || (tmp = kthAncestor(root->left,cur,k)) || (tmp = kthAncestor(root->right,cur,k))){
    if(k)k--;
    else if (k == 0){
      cout<<"kth ancestor of "<<cur<<" is "<<root->data;
      return NULL;
    }
    return root;
  }
}

int main()
{
  node* root = create(5);
  root->left = create(7);
  root->right = create(3);
  root->left->left = create(9);
  root->left->right = create(6);
  root->left->right->left = create(1);
  root->left->right->right = create(4);
  int k = 2;
  kthAncestor(root, 4, k);
}

kth ancestor of 4 is 7

Java code to find Kth ancestor of a node in binary tree

import java.util.*;
class node{
  int data;
  node left, right;
}
class Main{

  static node create(int data){
    node tmp = new node();
    tmp.data = data;
    tmp.left = tmp.right = null;
    return tmp;
  }

  	static int k = 2;
  static node tmp = null;

  static node kthAncestor(node root, int cur)
  {
    if (root == null)
      return null;
    if ((root.data == cur) || ((tmp = kthAncestor(root.left,cur)) != null) || ((tmp = kthAncestor(root.right,cur)) != null)){
      if(k > 0)k--;
      else if (k == 0){
        System.out.print("kth ancestor of "+cur+" is "+root.data);
        return null;
      }
      return root;
    }
    return null;
  }

  public static void main(String[] args)
  {
    node root = create(5);
    root.left = create(7);
    root.right = create(3);
    root.left.left = create(9);
    root.left.right = create(6);
    root.left.right.left = create(1);
    root.left.right.right = create(4);
    k = 2;
    kthAncestor(root, 4);
  }
}

kth ancestor of 4 is 7

Complexity Analysis

Time Complexity

O(N), because in the worst case may have to traverse all the nodes before which we find the required node.

Space Complexity

O(N), because of compiler stack which is being used for the recursive functions.