Table of Contents
Problem Statement
“K’th Largest element in BST using constant extra space” states that you are given a binary search tree and you need to find the kth largest element in it. So if we arrange the elements of the binary search tree in descending order then we need to return the kth number from the sequence.
Example
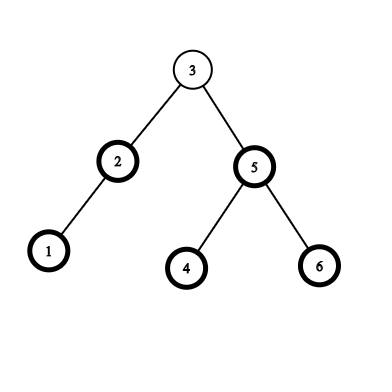
k=4
3
Explanation: If the elements are arranged in the descending order, the sequence is [6, 5, 4, 3, 2, 1]. Now the fourth largest element is the element at the fourth index that is 3.
Approach to find K’th Largest element in BST using constant extra space
Naive approach
We can solve this problem by first storing the inorder traversal and then finding the n-k+1 element in the sequence will result in the answer to the problem. But this approach will have O(N) space complexity. We also discussed a more efficient solution where we did a reverse inorder traversal and kept a count for the number of nodes. While counting the nodes we were also checking if we node count is equal to k. If the node count is equal to k, we return the node. Else, in the end, we return a message that the kth largest node is not found.
Efficient Approach
In the previous approach, we used reverse inorder traversal which required O(H) space for recursion. We can do the same thing as we did with the inorder traversal. As we reversed the inorder traversal. We will use Morris traversal for doing the inorder traversal in O(1) space. but instead of simply doing this we will do the reverse in-order traversal using Morris Traversal.
Morris Traversal is used on the binary threaded tree, the binary threaded tree is nothing but a binary tree having an extra thread. This makes it easier to perform traversal on the tree. Reverse Morris Traversal is just Morris Traversal but in a reverse manner. In normal morris traversal, we would have first moved to left subtree and then to right subtree. But here first we move to right subtree and then to left subtree. This way can perform the traversal in descending order. And then we return the kth element from the start. That is we keep a count and when the count is equal to k we return that element.
Code
C++ code to find K’th Largest element in BST using constant extra space
#include <bits/stdc++.h>
using namespace std;
struct node{
int data;
node *left;
node *right;
} ;
node* create(int data){
node * tmp = new node();
tmp->data = data;
tmp->left = tmp->right = NULL;
return tmp;
}
// normally insert the node in BST
node* insert(node* root, int x)
{
if (root == NULL)
return create(x);
if(x<root->data)
root->left = insert(root->left, x);
else if(x>root->data)
root->right = insert(root->right, x);
return root;
}
node* findKthLargest(node* root, int k)
{
node *cur = root; node* kLargest = NULL;
int cnt = 0;
while(cur != NULL){
// if right subtree is NULL, then move to left subtree
if(cur->right == NULL){
// if current node is kth largest
if(cnt == k-1)
kLargest = cur;
cnt++;
// move to the left subtree
cur = cur->left;
}
else{
// to find successor of current node
node* successor = cur->right;
while(successor->left != NULL && successor->left != cur)
successor = successor->left;
if(successor->left == NULL){
// set current node as left child of successor as it doesn't have left child
successor->left = cur;
cur = cur->right;
}
else{
// remove threads to restore the original tree
successor->left = NULL;
if(cnt == k-1)
kLargest = cur;
cnt++;
cur = cur->left;
}
}
}
return kLargest;
}
int main()
{
node *root = NULL;
int n;cin>>n;
for(int i=0;i<n;i++){
int element;cin>>element;
root = insert(root, element);
}
int k;cin>>k;
node* res = findKthLargest(root, k);
if(res == NULL)
cout<<"No kth largest found";
else
cout<<"Kth largest element is "<<res->data;
}
6 3 2 1 5 4 6 4
Kth largest element is 3
Java code to find K’th Largest element in BST using constant extra space
import java.util.*;
import java.lang.*;
import java.io.*;
class node{
int data;
node left;
node right;
}
class Tree{
static node root;
static int count;
static node create(int data){
node tmp = new node();
tmp.data = data;
tmp.left = null;
tmp.right = null;
return tmp;
}
static node insert(node root, int x)
{
if (root == null)
return create(x);
if(x<root.data)
root.left = insert(root.left, x);
else if(x>root.data)
root.right = insert(root.right, x);
return root;
}
static node findKthLargest(node root, int k)
{
node cur = root; node kLargest = null;
int cnt = 0;
while(cur != null){
// if right subtree is NULL, then move to left subtree
if(cur.right == null){
// if current node is kth largest
if(cnt == k-1)
kLargest = cur;
cnt++;
// move to the left subtree
cur = cur.left;
}
else{
// to find successor of current node
node successor = cur.right;
while(successor.left != null && successor.left != cur)
successor = successor.left;
if(successor.left == null){
// set current node as left child of successor as it doesn't have left child
successor.left = cur;
cur = cur.right;
}
else{
// remove threads to restore the original tree
successor.left = null;
if(cnt == k-1)
kLargest = cur;
cnt++;
cur = cur.left;
}
}
}
return kLargest;
}
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for(int i=0;i<n;i++){
int element = sc.nextInt();
root = insert(root, element);
}
int k = sc.nextInt();
count = 0;
node res = findKthLargest(root, k);
if(res == null)
System.out.println("No kth largest found");
else
System.out.println("Kth largest element is "+res.data);
}
}
6 3 2 1 5 4 6 4
Kth largest element is 3
Complexity Analysis
Time Complexity
O(N), because we have once traversed over all the elements of the tree. The time complexity is linear i.e. O(N).
Space Complexity
O(1), because we have used morris traversal instead of doing the traversal recursively.