In this problem we have given a binary tree, print its level order traversal in a spiral form.
Table of Contents
Examples
Input
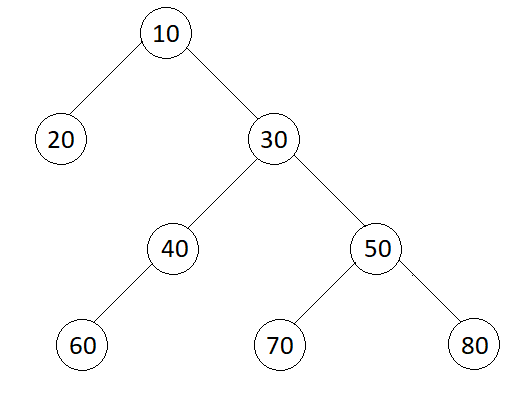
Output
10 30 20 40 50 80 70 60
Naive Approach for Level order Traversal in Spiral Form
The idea is to do a normal level order traversal using a queue, and use a stack to print the required levels in reverse order.
Level 1 is not reversed, level 2 is reversed, level 3 is not reversed, and so on. For all the levels that are to be printed in reverse order, add all the elements of that level to a stack and then print them.
- Create a queue and push the root to it. Initialize a boolean variable reverse as false.
- While the queue is not empty, repeat steps
- Initialize a variable size as the size of the queue. Run a loop from 1 to size, and at every iteration remove an element from the queue and if the reverse is true, push it to a stack, else print it. Also, push the children of removed elements into the queue.
- If the reverse is true, print the elements of the stack.
- Negate reverse, that is, if the reverse is true, make it false, and if the reverse is false, make it true.
JAVA Code
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
public class Naive {
// class representing a tree node
static class Node {
int data;
Node left, right;
public Node(int data) {
this.data = data;
}
}
private static void spiralOrderTraversal(Node root) {
if (root == null) {
return;
}
// create a queue for level order traversal
Queue<Node> queue = new LinkedList<>();
// create a stack (used to print a level in reverse order)
Stack<Node> stack = new Stack<>();
// Initially reverse is false
boolean reverse = false;
// add the root to the queue
queue.add(root);
// Do a normal level order traversal
while (!queue.isEmpty()) {
int size = queue.size();
// Traverse current level
for (int i = 0; i < size; i++) {
Node curr = queue.poll();
// if reverse is true, push the element to stack, else print it
if (reverse) {
stack.push(curr);
} else {
System.out.print(curr.data + " ");
}
if (curr.left != null) {
queue.add(curr.left);
}
if (curr.right != null) {
queue.add(curr.right);
}
}
// if this level has to be reversed, print the content of the stack
if (reverse) {
while (!stack.isEmpty()) {
System.out.print(stack.pop().data + " ");
}
}
// negate reverse
reverse = !reverse;
}
}
public static void main(String[] args) {
// Example tree
Node root = new Node(10);
root.left = new Node(20);
root.right = new Node(30);
root.right.left = new Node(40);
root.right.right = new Node(50);
root.right.left.left = new Node(60);
root.right.right.left = new Node(70);
root.right.right.right = new Node(80);
spiralOrderTraversal(root);
}
}10 30 20 40 50 80 70 60
C++ Code
#include<bits/stdc++.h>
using namespace std;
// class representing a tree node
class Node {
public:
int data;
Node *left;
Node *right;
Node(int d) {
data = d;
left = right = NULL;
}
};
// function to create a new node
Node* newNode(int x) {
Node *node = new Node(x);
return node;
}
void spiralOrderTraversal(Node *root) {
if (root == NULL) {
return;
}
// create a queue for level order traversal
queue<Node*> q;
// create a stack (used to print a level in reverse order)
stack<Node*> st;
// Initially reverse is false
bool reverse = false;
// add the root to the queue
q.push(root);
// Do a normal level order traversal
while (!q.empty()) {
int size = q.size();
// Traverse current level
for (int i = 0; i < size; i++) {
Node* curr = q.front();
q.pop();
// if reverse is true, push the element to stack, else print it
if (reverse) {
st.push(curr);
} else {
cout<<curr->data<<" ";
}
if (curr->left != NULL) {
q.push(curr->left);
}
if (curr->right != NULL) {
q.push(curr->right);
}
}
// if this level has to be reversed, print the content of the stack
if (reverse) {
while (!st.empty()) {
cout<<st.top()->data<<" ";
st.pop();
}
}
// negate reverse
reverse = !reverse;
}
}
int main() {
// Example Tree
Node *root = newNode(10);
root->left = newNode(20);
root->right = newNode(30);
root->right->left = newNode(40);
root->right->right = newNode(50);
root->right->left->left = newNode(60);
root->right->right->left = newNode(70);
root->right->right->right = newNode(80);
spiralOrderTraversal(root);
}10 30 20 40 50 80 70 60
Complexity Analysis for Level order Traversal in Spiral Form
Time Complexity = O(n), the upper bound on the time complexity is (4 * n)
Space Complexity = O(n)
Optimal Approach for Level order Traversal in Spiral Form
We use two stacks to print the level order traversal. Let us call them as st1 and st2 respectively.
st1 prints out the usual level order traversal and st2 prints the reversed level order traversal.
- Push the root in st1.
- Do the following, while either st1 or st2 is not empty,
- While st1 is not empty, pop out an element and print it, and push its left and right children to st2.
- While st2 is not empty, pop out an element and print it, and push its right and left children to st1, notice the reverse order, that is, first push the right child and then the left child.
JAVA Code
import java.util.Stack;
public class LevelOrderTraversalInSpiralForm {
// class representing a tree node
static class Node {
int data;
Node left, right;
public Node(int data) {
this.data = data;
}
}
private static void spiralOrderTraversal(Node root) {
if (root == null) {
return;
}
// Create two stacks
Stack<Node> st1 = new Stack<>();
Stack<Node> st2 = new Stack<>();
// push the root to st1
st1.push(root);
// do the following while either st1 is not empty or st2 is not empty
while (!st1.isEmpty() || !st2.isEmpty()) {
// while st1 is not empty
while (!st1.isEmpty()) {
// pop the current element and print it
Node curr = st1.pop();
System.out.print(curr.data + " ");
// push its children to st2
if (curr.left != null)
st2.push(curr.left);
if (curr.right != null)
st2.push(curr.right);
}
// while st2 is not empty
while (!st2.isEmpty()) {
// pop the current element and print it
Node curr = st2.pop();
System.out.print(curr.data + " ");
// Push its right child and left child to st1 respectively
if (curr.right != null)
st1.push(curr.right);
if (curr.left != null)
st1.push(curr.left);
}
}
System.out.println();
}
public static void main(String[] args) {
// Example tree
Node root = new Node(10);
root.left = new Node(20);
root.right = new Node(30);
root.right.left = new Node(40);
root.right.right = new Node(50);
root.right.left.left = new Node(60);
root.right.right.left = new Node(70);
root.right.right.right = new Node(80);
spiralOrderTraversal(root);
}
}10 30 20 40 50 80 70 60
C++ Code
#include<bits/stdc++.h>
using namespace std;
// class representing a tree node
class Node {
public:
int data;
Node *left;
Node *right;
Node(int d) {
data = d;
left = right = NULL;
}
};
// function to create a new node
Node* newNode(int x) {
Node *node = new Node(x);
return node;
}
void spiralOrderTraversal(Node *root) {
if (root == NULL) {
return;
}
// Create two stacks
stack<Node*> st1;
stack<Node*> st2;
// push the root to st1
st1.push(root);
// do the following while either st1 is not empty or st2 is not empty
while (!st1.empty() || !st2.empty()) {
// while st1 is not empty
while (!st1.empty()) {
// pop the current element and print it
Node *curr = st1.top();
st1.pop();
cout<<curr->data<<" ";
// push its children to st2
if (curr->left != NULL)
st2.push(curr->left);
if (curr->right != NULL)
st2.push(curr->right);
}
// while st2 is not empty
while (!st2.empty()) {
// pop the current element and print it
Node *curr = st2.top();
st2.pop();
cout<<curr->data<<" ";
// Push its right child and left child to st1 respectively
if (curr->right != NULL)
st1.push(curr->right);
if (curr->left != NULL)
st1.push(curr->left);
}
}
cout<<endl;
}
int main() {
// Example Tree
Node *root = newNode(10);
root->left = newNode(20);
root->right = newNode(30);
root->right->left = newNode(40);
root->right->right = newNode(50);
root->right->left->left = newNode(60);
root->right->right->left = newNode(70);
root->right->right->right = newNode(80);
spiralOrderTraversal(root);
}10 30 20 40 50 80 70 60
Complexity Analysis for Level order Traversal in Spiral Form
Time Complexity = O(n), the upper bound on the time complexity is (2 * n)
Space Complexity = O(n)