Table of Contents
Problem Statement
Given Two Balanced Binary Search Trees, there are n elements in the first BST and m elements in the second BST. Write an algorithm to merge two balanced binary search trees to form a third balanced Binary Search Tree with (n + m) elements.
Example
Input
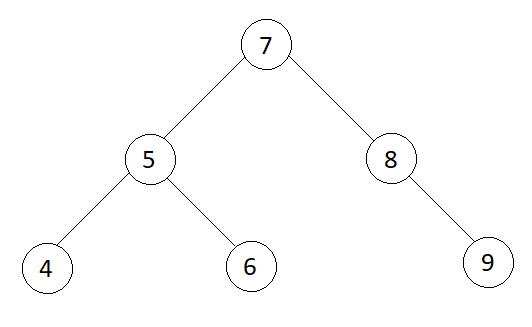
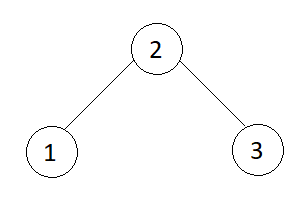
Output
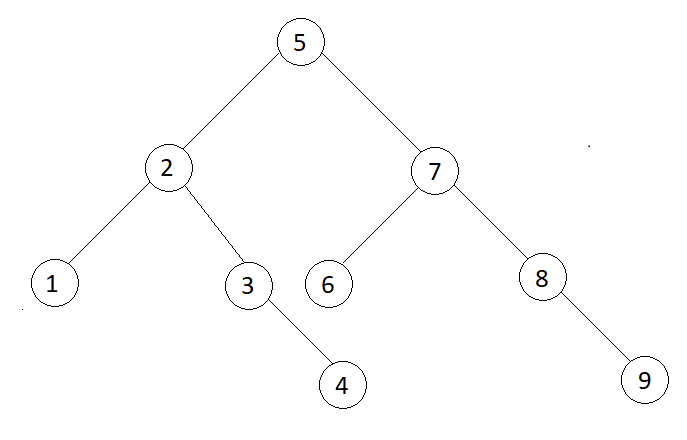
Pre-order : 5 2 1 3 4 7 6 8 9
Algorithm to merge two binary search trees
At first, it looks like that inserting all the elements from tree2 to tree1 one by one is the best solution. But this solution has a time complexity of O(n log(n)), there is a solution that can do better than this.
We now know how to convert a sorted array to a balanced binary tree, we are going to reduce the given problem to that problem.
The idea is to store the inorder traversal of both the trees in two arrays, say, arr1 and arr2 respectively. Now we create one more array that contains all the elements of arr1 and arr2 merged together in sorted form. Two sorted arrays can be merged to form a new sorted array in linear time complexity. We then convert the sorted array to a balanced binary search tree, hence the two trees are merged.
1. Store the in-order traversal of both the trees in two arrays, say, arr1 and arr2 respectively. 2. Merge arr1 and arr2 to form another array arr, that contains the elements of arr1 and arr2 in sorted form. 3. We now use this sorted array(arr) to build a balanced binary search tree, which is a merged version of the given trees. 4. The middle element of the array forms the root of the balanced BST and all the elements to the left of the middle element form the left sub-tree and all the elements to the right of the middle element form the right sub-tree. 5. Recursively do step 4 for the left subtree and attach it to the left of root. 6. Recursively do step 4 for the right subtree and attach it to the right of root. 7. Return root.
Time Complexity = O(n + m)
Since we have found the in-order traversal of the first and second array, this counts for O(n+m). Then merging these two sorted arrays again counts for O(n+m) time complexity. And making a new balanced binary search tree also takes O(n+m) time. Thus, totally we can say the solution has linear time complexity.
Space Complexity = O(N)
Here for this problem, we have a linear space complexity. Since we have stored three arrays one of size n, second of size m, and after the merging these sorted arrays. Again we have a sorted array of size n+m. After this when we make the final tree, then too we are dealing with only n+m nodes. Thus, we have a linear space complexity = O(N).
n -> number of nodes in tree1
m -> number of nodes in tree2
Code
JAVA Code to merge two BSTs
import java.util.ArrayList;
class MergeTwoBalancedBinarySearchTrees {
// class representing node of a binary tree
static class Node {
int data;
Node left, right;
public Node(int data) {
this.data = data;
}
}
// function to print pre-order traversal of a binary tree
private static void preOrder(Node root) {
if (root != null) {
System.out.print(root.data + " ");
preOrder(root.left);
preOrder(root.right);
}
}
// function to store in-order traversal of a binary tree in an array-list
private static void storeInOrder(Node root, ArrayList<Integer> arr) {
if (root != null) {
storeInOrder(root.left, arr);
arr.add(root.data);
storeInOrder(root.right, arr);
}
}
// function to merge two sorted array-lists
private static ArrayList<Integer> mergeSortedArrays(ArrayList<Integer> arr1, ArrayList<Integer> arr2) {
int i = 0, j = 0;
ArrayList<Integer> arr = new ArrayList<>();
while (i < arr1.size() && j < arr2.size()) {
if (arr1.get(i) < arr2.get(j)) {
arr.add(arr1.get(i));
i++;
} else {
arr.add(arr2.get(j));
j++;
}
}
while (i < arr1.size()) {
arr.add(arr1.get(i));
i++;
}
while (j < arr2.size()) {
arr.add(arr2.get(j));
j++;
}
return arr;
}
// function to convert sorted array-list to balanced BST
private static Node constructBSTFromSortedArray(ArrayList<Integer> arr, int start, int end) {
// base case
if (start > end) {
return null;
}
int mid = (start + end) / 2;
Node root = new Node(arr.get(mid));
root.left = constructBSTFromSortedArray(arr, start, mid - 1);
root.right = constructBSTFromSortedArray(arr, mid + 1, end);
return root;
}
private static Node mergeBST(Node root1, Node root2) {
// store the in-order traversal of tree1 in an array
ArrayList<Integer> arr1 = new ArrayList<>();
storeInOrder(root1, arr1);
// store the in-order traversal of tree2 in an array
ArrayList<Integer> arr2 = new ArrayList<>();
storeInOrder(root2, arr2);
// merge the two sorted arrays
ArrayList<Integer> arr = mergeSortedArrays(arr1, arr2);
// construct the balanced BST from this sorted array
return constructBSTFromSortedArray(arr, 0, arr.size() - 1);
}
public static void main(String[] args) {
// Example
Node root1 = new Node(7);
root1.left = new Node(5);
root1.right = new Node(8);
root1.left.left = new Node(4);
root1.left.right = new Node(6);
root1.right.right = new Node(9);
Node root2 = new Node(2);
root2.left = new Node(1);
root2.right = new Node(3);
Node root = mergeBST(root1, root2);
preOrder(root);
System.out.println();
}
}5 2 1 3 4 7 6 8 9
C++ Code to merge two BSTs
#include <bits/stdc++.h>
using namespace std;
// class representing node of a binary tree
class Node {
public:
int data;
Node *left;
Node *right;
Node(int d) {
data = d;
left = right = NULL;
}
};
// function to print pre-order traversal of a binary tree
void preOrder(Node *root) {
if (root != NULL) {
cout<<root->data<<" ";
preOrder(root->left);
preOrder(root->right);
}
}
// function to store the inorder traversal of tree in a list
void storeInOrder(Node *root, vector<int> &arr) {
if (root != NULL) {
storeInOrder(root->left, arr);
arr.push_back(root->data);
storeInOrder(root->right, arr);
}
}
// function to merge two sorted array-lists
vector<int> mergeSortedArrays(vector<int> &arr1, vector<int> &arr2) {
int i = 0, j = 0;
vector<int> arr;
while (i < arr1.size() && j < arr2.size()) {
if (arr1[i] < arr2[j]) {
arr.push_back(arr1[i]);
i++;
} else {
arr.push_back(arr2[j]);
j++;
}
}
while (i < arr1.size()) {
arr.push_back(arr1[i]);
i++;
}
while (j < arr2.size()) {
arr.push_back(arr2[j]);
j++;
}
return arr;
}
// function to convert sorted array-list to balanced BST
Node* constructBSTFromSortedArray(vector<int> &arr, int start, int end) {
// base case
if (start > end) {
return NULL;
}
int mid = (start + end) / 2;
Node *root = new Node(arr[mid]);
root->left = constructBSTFromSortedArray(arr, start, mid - 1);
root->right = constructBSTFromSortedArray(arr, mid + 1, end);
return root;
}
Node* mergeBST(Node *root1, Node *root2) {
// store the in-order traversal of tree1 in an array
vector<int> arr1;
storeInOrder(root1, arr1);
// store the in-order traversal of tree2 in an array
vector<int> arr2;
storeInOrder(root2, arr2);
// merge the two sorted arrays
vector<int> arr = mergeSortedArrays(arr1, arr2);
// construct the balanced BST from this sorted array
return constructBSTFromSortedArray(arr, 0, arr.size() - 1);
}
int main() {
// Example
Node *root1 = new Node(7);
root1->left = new Node(5);
root1->right = new Node(8);
root1->left->left = new Node(4);
root1->left->right = new Node(6);
root1->right->right = new Node(9);
Node *root2 = new Node(2);
root2->left = new Node(1);
root2->right = new Node(3);
Node *root = mergeBST(root1, root2);
preOrder(root);
cout<<endl;
return 0;
}5 2 1 3 4 7 6 8 9