Table of Contents
Problem Statement
The problem “Number of siblings of a given Node in n-ary Tree” states that you are given an n-ary Tree and a target node. Find the number of siblings of the target node. Assume that node is always present in the tree and the first node is the root of the tree.
Example
Input
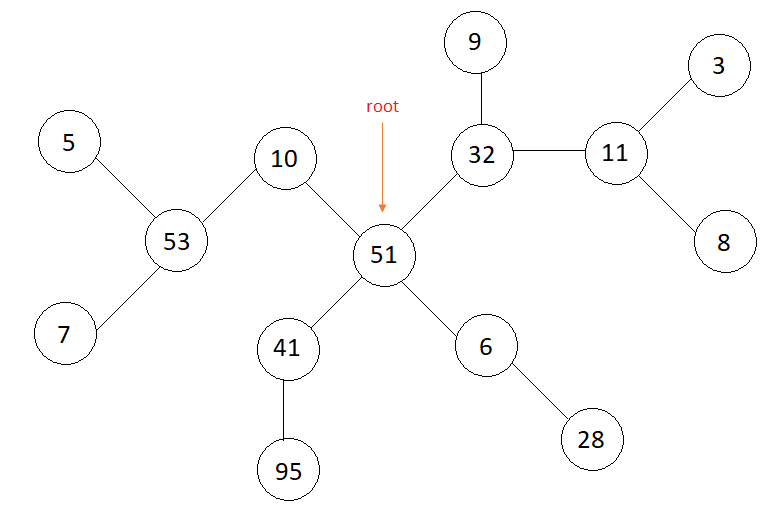
node = 10
node = 11
3 1
Explanation
Siblings of 10 are {41, 6, 32}
Siblings of 11 are {9}
Algorithm
Siblings of a node are the nodes present at the same level as the given node, or in other words, siblings of a node are one less than the number of children of its parent.
Consider the tree in above example, and let the node be 10
Parent of 10 = 51
Children of 51 are {10, 41, 32, 6}
Siblings of 10 are children of its parent except 10, that is, siblings of 10 are {41, 32, 6}
Important Point: The number of siblings of the root is 0. Because there is no parent of root.
The idea to find the number of siblings of a node is to do a BFS on the given tree, if a node’s children is the same as the given node, return (number of children of that node – 1).
- If the given node is equals to the root or root is null, return 0.
- Create a queue of nodes for BFS and push the root to the queue.
- While the queue is not empty repeat step 4.
- Remove an element from the queue, traverse through all the children of the current element, if any of its children is equals to the given node, return (number of children of current node – 1), else push the children to the queue.
- If there is no node matching the given node, return -1.
Code
Java Code to find Number of siblings of a given Node in n-ary Tree
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
class NumberOfSiblingsOfAGivenNodeInNAryTree {
// class representing node of n-ary tree
static class Node {
ArrayList<Node> child;
int data;
public Node(int data) {
this.data = data;
this.child = new ArrayList<>();
}
}
private static int siblings(Node root, int target) {
// if the given node is equals to the root or root is null, return 0
if (root == null || root.data == target) {
return 0;
}
// create a queue of nodes
Queue<Node> queue = new LinkedList<>();
// push the root to queue
queue.add(root);
// do a BFS of the tree
while (!queue.isEmpty()) {
// remove one element from the queue
Node curr = queue.poll();
// traverse its children
for (int i = 0; i < curr.child.size(); i++) {
// current child
Node currChild = curr.child.get(i);
// if current child is the target, return (parent's children count - 1)
if (currChild.data == target) {
return (curr.child.size() - 1);
}
// add the child to the queue
queue.add(currChild);
}
}
// if there is no match, return -1
return -1;
}
public static void main(String[] args) {
// Example n-ary tree
Node root = new Node(51);
// children of 51
root.child.add(new Node(10));
root.child.add(new Node(41));
root.child.add(new Node(6));
root.child.add(new Node(32));
// children of 10
root.child.get(0).child.add(new Node(53));
// children of 41
root.child.get(1).child.add(new Node(95));
// children of 6
root.child.get(2).child.add(new Node(28));
// children of 32
root.child.get(3).child.add(new Node(9));
root.child.get(3).child.add(new Node(11));
// children of 53
root.child.get(0).child.get(0).child.add(new Node(5));
root.child.get(0).child.get(0).child.add(new Node(7));
// children of 11
root.child.get(3).child.get(1).child.add(new Node(3));
root.child.get(3).child.get(1).child.add(new Node(8));
System.out.println(siblings(root, 10));
System.out.println(siblings(root, 11));
}
}3 1
C++ Code to find Number of siblings of a given Node in n-ary Tree
#include <bits/stdc++.h>
using namespace std;
// class representing node of a n-ary tree
class Node {
public:
int data;
vector<Node*> child;
Node(int d) {
data = d;
}
};
int siblings(Node *root, int target) {
// if the given node is equals to the root or root is null, return 0
if (root == NULL || root->data == target) {
return 0;
}
// create a queue of nodes
queue<Node*> q;
// push the root to queue
q.push(root);
// do a BFS of the tree
while (!q.empty()) {
// remove one element from the queue
Node *curr = q.front();
q.pop();
// traverse its children
for (int i = 0; i < curr->child.size(); i++) {
// current child
Node *currChild = curr->child[i];
// if current child is the target, return (parent's children count - 1)
if (currChild->data == target) {
return (curr->child.size() - 1);
}
// add the child to the queue
q.push(curr->child[i]);
}
}
// if there is no match, return -1
return -1;
}
int main() {
// Example n-ary tree
Node *root = new Node(51);
// children of 51
root->child.push_back(new Node(10));
root->child.push_back(new Node(41));
root->child.push_back(new Node(6));
root->child.push_back(new Node(32));
// children of 10
root->child[0]->child.push_back(new Node(53));
// children of 41
root->child[1]->child.push_back(new Node(95));
// children of 6
root->child[2]->child.push_back(new Node(28));
// children of 32
root->child[3]->child.push_back(new Node(9));
root->child[3]->child.push_back(new Node(11));
// children of 53
root->child[0]->child[0]->child.push_back(new Node(5));
root->child[0]->child[0]->child.push_back(new Node(7));
// children of 11
root->child[3]->child[1]->child.push_back(new Node(3));
root->child[3]->child[1]->child.push_back(new Node(8));
cout<<siblings(root, 10)<<endl;
cout<<siblings(root, 11)<<endl;
return 0;
}3 1
Complexity Analysis
Time Complexity
O(N), because we have done BFS for tree. We have just traversed over all the nodes which made the algorithm to run in linear time.
Space Complexity
O(N), using a queue for BFS has cost us linear space. Thus the space complexity of the algorithm is O(N).