Given a binary tree and a specific node or key. Print ancestors of a given binary tree node without recursion.
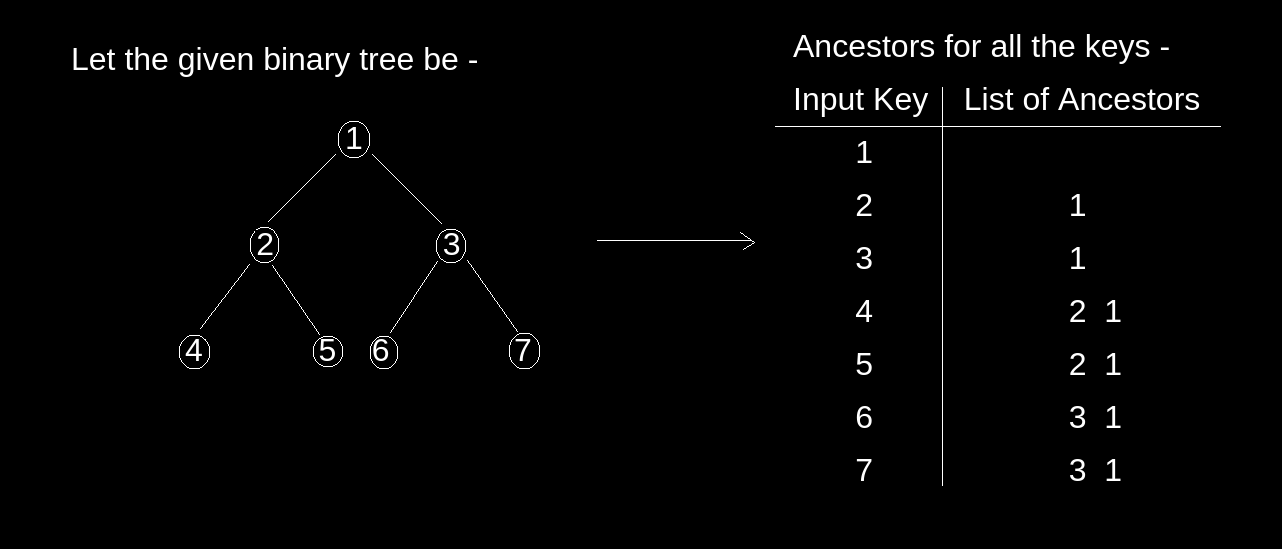
Table of Contents
Example
Input :
key = 7
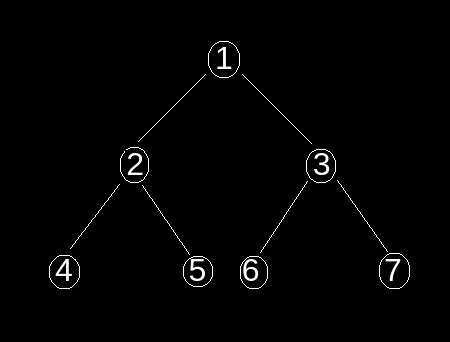
Output : 3 1
Input :
key = 4
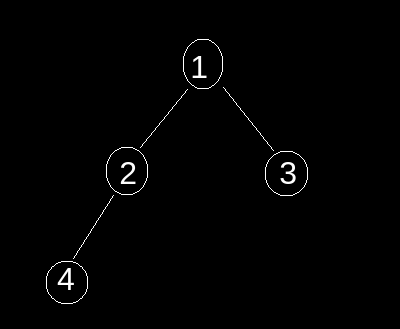
Output : 2 1
Algorithm for Ancestors of a Given Binary Tree Node
- Create a class Node which contains an integer variable to hold data and two Node type objects left and right. Create the parameterized constructor inside it which accepts an integer value as it’s a parameter and store it in the integer variable of the class node.
- After that, create the function to print the ancestors of the given key which accepts the root node of the tree and the key as it’s a parameter.
- Check if the root is equal to null, return. Else create a stack data structure of type node.
- Start traversing the given binary tree.
- While root is not equal to null and the data of the root is not equal to the given key, push the root in the stack and update the root as left of root.
- If the root is not equal to null and the data of the root is equal to the given key, break the loop.
- Else if the right of the node at the top of the stack is equal to null, update the root at the node at the top of the stack and pop the top of the stack. While the stack is not empty and the right of the node at the top of the stack is equal to the root, update the root at the node at the top of the stack and pop the top of the stack.
- If the stack is empty, update the root as null else update the root as the right of the node at the top of the stack.
- While the stack is not empty, print the data of the node at the top of the stack and pop the top of the stack.
C++ Program for Ancestors of a Given Binary Tree Node
#include <bits/stdc++.h>
using namespace std;
struct Node{
int data;
struct Node *left, *right;
};
struct Node* newNode(int data){
struct Node* node = (struct Node*) malloc(sizeof(struct Node));
node->data = data;
node->left = node->right = NULL;
return node;
}
void printAncestors(struct Node *root, int key){
if(root == NULL){
return;
}
stack<struct Node* > st;
while(1){
while(root && root->data != key){
st.push(root);
root = root->left;
}
if(root && root->data == key){
break;
}
if(st.top()->right == NULL){
root = st.top();
st.pop();
while(!st.empty() && st.top()->right == root){
root = st.top();
st.pop();
}
}
root = st.empty()? NULL: st.top()->right;
}
while(!st.empty()){
cout<<st.top()->data<<" ";
st.pop();
}
}
int main(){
struct Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
int key = 7;
printAncestors(root, key);
return 0;
}3 1
Java Program for Ancestors of a Given Binary Tree Node
import java.util.Stack;
class findAncestors{
static class Node{
int data;
Node left,right;
Node(int data){
this.data = data;
}
}
static void printAncestors(Node root,int key){
if(root == null){
return;
}
Stack<Node> st = new Stack<>();
while(true){
while(root != null && root.data != key){
st.push(root);
root = root.left;
}
if(root != null && root.data == key){
break;
}
if(st.peek().right == null){
root =st.peek();
st.pop();
while( st.empty() == false && st.peek().right == root){
root = st.peek();
st.pop();
}
}
root = st.empty() ? null : st.peek().right;
}
while(!st.empty()){
System.out.print(st.peek().data+" ");
st.pop();
}
}
public static void main(String[] args){
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
int key = 7;
printAncestors(root, key);
}
}3 1
Complexity Analysis
Time Complexity: O(n) where n is the number of nodes inserted.
Space Complexity: O(n) because we used space for n nodes.