Reverse a Path in BST using Queue

In reverse a path in BST using queue problem we have given a Binary Search Tree and node, write an algorithm to reverse the path from root to the given node. Assume that the node exists in the BST.

Example

Input

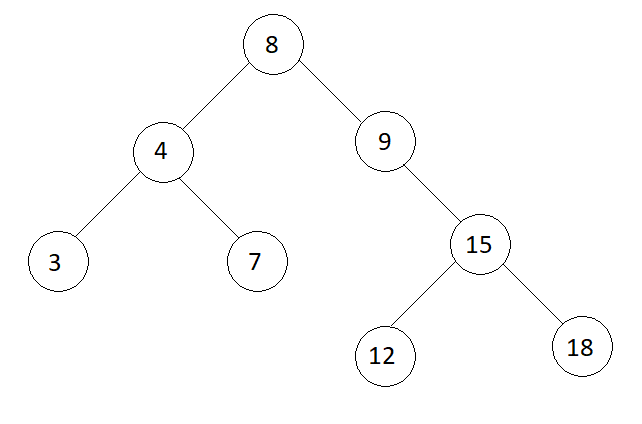
Target Node = 12
Output

In-order traversal before the reversal
3 4 7 8 9 12 15 18
In-order traversal after reversal
3 4 7 12 15 8 9 18

Algorithm for Reverse a Path in BST using Queue

Reversing a path from the root to the node is same as reversing the elements of the nodes on the path from the root to the node. For example, if the path from the root to the node is 5 -> 10 -> 15 -> 20, then reversing the path is the same as reversing the data. So the reversed path is 20 ->15 -> 10 -> 5.
The idea is to push all the values of nodes that come in the path from the root to the given node in a queue and after pushing replace the current node with the element at the front of the queue.

reversePathBST(root, target)

1. If the root is null, return.
2. If root’s value equals to the target, then push the root’s value to the queue and replace the root’s value with the element at the queue front. Remove the element at front of the queue.
3. Else if root’s value is less than the target, then push the root’s value to the queue, call reversePathBST recursively for root’s left child and then replace root’s value with the element at front of the queue. Also, remove the element at the front of the queue.
4. Else push the root’s value to the queue, call reversePathBST recursively for root’s right child and then replace root’s value by element present at the front of the queue. Also, remove the element at the front of the queue.

JAVA Code for Reverse a Path in BST using Queue

import java.util.LinkedList;
import java.util.Queue;

public class ReverseAPathInBSTUsingQueue {
    // class representing node of a BST
    static class Node {
        int data;
        Node left, right;

        public Node(int data) {
            this.data = data;
        }
    }

    // queue used to reverse the path in BST
    private static Queue<Integer> queue;

    // function to print inorder traversal of a tree
    private static void inorder(Node root) {
        if (root != null) {
            inorder(root.left);
            System.out.print(root.data + " ");
            inorder(root.right);
        }
    }

    private static void reversePath(Node root, int target) {
        // if root is null return
        if (root == null) {
            return;
        }

        // add root's data to queue
        queue.add(root.data);

        if (root.data == target) {
            // Base case
        } else if (root.data > target) {
            // target is in left sub tree
            reversePath(root.left, target);
        } else {
            // target is in right sub tree
            reversePath(root.right, target);
        }

        // replace root's data with front of queue
        root.data = queue.poll();
    }

    public static void main(String[] args) {
        // Example Tree
        Node root = new Node(8);
        root.left = new Node(4);
        root.right = new Node(9);
        root.left.left = new Node(3);
        root.left.right = new Node(7);
        root.right.right = new Node(15);
        root.right.right.left = new Node(12);
        root.right.right.right = new Node(18);

        // inorder traversal before reversing
        System.out.println("Inorder before reversal");
        inorder(root);
        System.out.println();

        queue = new LinkedList<>();
        reversePath(root, 12);

        // inorder traversal after reversing
        System.out.println("Inorder after reversal");
        inorder(root);
        System.out.println();
    }
}

Inorder before reversal
3 4 7 8 9 12 15 18 
Inorder after reversal
3 4 7 12 15 8 9 18

C++ Code for Reverse a Path in BST using Queue

#include <bits/stdc++.h>
using namespace std;

// class representing node of a BST
class Node {
    public:
    int data;
    Node *left;
    Node *right;
    
    Node(int d) {
        data = d;
        left = right = NULL;
    }
};

// queue used to reverse the path in BST
queue<int> q;

void inorder(Node *root) {
    if (root != NULL) {
        inorder(root->left);
        cout<<root->data<<" ";
        inorder(root->right);
    }
}

void reversePath(Node *root, int target) {
    // if root is null return
    if (root == NULL) {
        return;
    }
    
    // add root's data to queue
    q.push(root->data);
    
    if (root->data == target) {
        // Base case
    } else if (root->data > target) {
        // target is in left sub tree
        reversePath(root->left, target);
    } else {
        // target is in right sub tree
        reversePath(root->right, target);
    }
    
    // replace root's data with front of queue
    root->data = q.front();
    q.pop();
}

int main() {
    // Example Tree
    Node *root = new Node(8);
    root->left = new Node(4);
    root->right = new Node(9);
    root->left->left = new Node(3);
    root->left->right = new Node(7);
    root->right->right = new Node(15);
    root->right->right->left = new Node(12);
    root->right->right->right = new Node(18);

    // inorder traversal before reversing
    cout<<"Inorder before reversal"<<endl;
    inorder(root);
    cout<<endl;
    
    reversePath(root, 12);

    // inorder traversal after reversing
    cout<<"Inorder after reversal"<<endl;
    inorder(root);
    cout<<endl;
    
    return 0;
}

Inorder before reversal
3 4 7 8 9 12 15 18 
Inorder after reversal
3 4 7 12 15 8 9 18

Complexity Analysis

Time Complexity = O(log n)
Space Complexity = O(log n)
where n is the number of nodes in the Binary Search Tree.

References