If we have performing addition on a given range of array whose element values updated any time. Then in that type of problem, we handle using a segment tree structure. Given an array a[] with n elements and you have to answer multiple queries, each of the queries is one of the two types :
1. 1 i x: Set a[i] = x
2. 2 l r: Find and print the sum of elements between l and r both inclusive
Table of Contents
Example
Input :
a[] = {2, 5, 9, 8, 11, 3}
q = 3 (Number of queries)
2 3 5
1 2 8
2 0 5
Output :
22
37
The naive approach to solve the above problem is to run a loop from l to r to and find the sum of the range and for updating, we directly set the value of a[i] as x.
Segment Tree Approach and Representation
- Leaf nodes of the segment tree are the elements of the given array.
- Each internal node stores the sum of its children.
A segment tree is represented as an array in memory, it is a full binary tree as every node has either 2 or 0 children and all levels are filled except possibly the last level. When represented as array there are some spaces that are never been used, hence the size of a segment tree is (2*x – 1), where x is the smallest power of 2 greater than or equal to n.
Segment Tree for the above example is shown in the image.
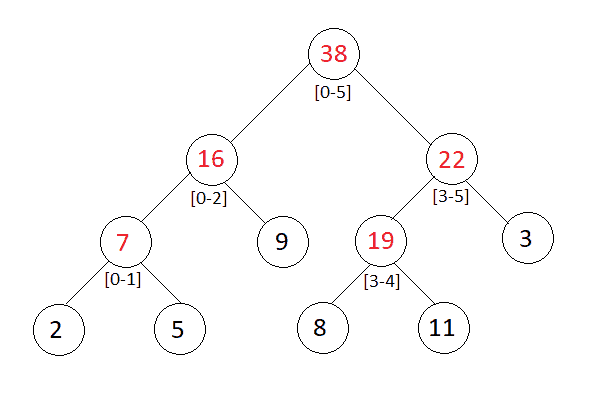
Construction
- We first allocate a memory equals to the size of the segment tree, that is, create an array of size equals the size of the segment tree.
- Then, for every node, the value of this node is equal to the sum of its left and right child.
- So, we write a recursive code to find the value of each node,
value[i] = value[2 * i + 1] + value[2 * i + 2] // Left child of i is (2*i + 1) and Right child is (2*i + 2) - The base case of the recurrence is when it is a leaf node, for the leaf node the value of node is equals to the value present in the array because both of its child are null(or absent).
Updating an element(Type-1 Query)
Let the ith index has to be updated to x and its original value was y, that is we have to increase its value by (x – y), and also all the sums containing this index in their range will also have to be incremented by (x – y), so we write a recursive code to do that,
- Start from the root.
- If the current node contains i within its range, then increment the value by (x- y) and recur for it’s left and right child.
- If the current node does not contain i within its range, then we do not make any changes to it
Sum range Query (Type-2 Query)
- Start from the root node, if the node range is between l and r return the value of this node.
- If the node’s range is completely outside the range l and r, return 0.
- In all the other cases return the sum of answers of the query(l, r) for it’s left child and it’s a right child.
JAVA Code for range sum using Segment Tree
public class SegmentTree {
// Function to find the sum of given range in the segment tree
// tree[] --> Segment Tree
// s --> Starting index of segment tree
// e --> Ending index of segment tree
// i --> Current index of segment tree
// l --> Lower index of range
// r --> Higher index of range
private static int rangeSum(int tree[], int s, int e, int l, int r, int i) {
// If the current node range is within the range l and r, return its value
if (l <= s && r >= e)
return tree[i];
// If current node's range is completely outside the range l and r, return 0
if (e < l || s > r)
return 0;
// For all other cases return sum of answers to query for left and right child
// Left child index = 2 * i + 1
// Right child index = 2 * i + 2
int mid = (s + e) / 2;
return rangeSum(tree, s, mid, l, r, 2 * i + 1) +
rangeSum(tree, mid + 1, e, l, r, 2 * i + 2);
}
// Function to update the segment tree for a given index
// s --> Starting index of segment tree
// e --> Ending index of segment tree
// index --> Index to be changed in the original array
// diff --> This is to be added in the nodes that contains index in their range
// i --> Current index of Segment tree
private static void updateValue(int tree[], int s, int e, int index, int diff, int i) {
// If the current node does not contain index in its range, make no changes
if (index < s || index > e)
return;
// Current node contains the index in its range, update the current nodes and its children
// Left child index = 2 * i + 1
// Right child index = 2 * i + 2
tree[i] = tree[i] + diff;
if (s != e) {
int mid = (s + e) / 2;
updateValue(tree, s, mid, index, diff, 2 * i + 1);
updateValue(tree, mid + 1, e, index, diff, 2 * i + 2);
}
}
// A function to create the segment tree recursively between s and e
// i --> Index of current node in the segment tree
private static int constructSegmentTree(int tree[], int a[], int s, int e, int i) {
// Leaf node case
if (s == e) {
tree[i] = a[s];
return a[s];
}
// For all other nodes its value is sum of left and right child's value
// Left child index = 2 * i + 1
// Right child index = 2 * i + 2
int mid = (s + e) / 2;
tree[i] = constructSegmentTree(tree, a, s, mid, i * 2 + 1) +
constructSegmentTree(tree, a, mid + 1, e, i * 2 + 2);
// Return the value of current node
return tree[i];
}
// Driver function for segment tree approach
public static void main(String args[]) {
int a[] = {2, 5, 9, 8, 11, 3};
int n = a.length;
// Calculate the size of the segment tree
int x = (int) (Math.ceil(Math.log(n) / Math.log(2)));
int size = 2 * (int) Math.pow(2, x) - 1;
// Allocate memory for segment tree
int tree[] = new int[size];
// Construct the segment tree
constructSegmentTree(tree, a, 0, n - 1, 0);
// Queries
int q = 3;
int type[] = {2, 1, 2}; // Stores the type of query to process
int l[] = {3, 2, 0}; // Stores the index of element to be updated for type-1 query and lower range for type-2 query
int r[] = {5, 8, 5}; // Stores the new value of element for type-1 query and higher range for type-2 query
for (int j = 0; j < q; j++) {
if (type[j] == 1) {
// Type-1 query (Update the value of specified index)
int index = l[j];
int value = r[j];
int diff = value - a[index]; // This diff is to be added to all the range that contains the index
// Update the value in array a
a[index] = value;
// Update segment tree
updateValue(tree, 0, n - 1, index, diff, 0);
} else {
// Type-2 query (Find the Sum of given range)
int sum = rangeSum(tree, 0, n - 1, l[j], r[j], 0);
System.out.println(sum);
}
}
}
}C++ Code for range sum using Segment Tree
#include <bits/stdc++.h>
using namespace std;
// Function to find the sum of given range in the segment tree
// tree[] --> Segment Tree
// s --> Starting index of segment tree
// e --> Ending index of segment tree
// i --> Current index of segment tree
// l --> Lower index of range
// r --> Higher index of range
int rangeSum(int *tree, int s, int e, int l, int r, int i) {
// If the current node range is within the range l and r, return its value
if (l <= s && r >= e)
return tree[i];
// If current node's range is completely outside the range l and r, return 0
if (e < l || s > r)
return 0;
// For all other cases return sum of answers to query for left and right child
// Left child index = 2 * i + 1
// Right child index = 2 * i + 2
int mid = (s + e) / 2;
return rangeSum(tree, s, mid, l, r, 2 * i + 1) +
rangeSum(tree, mid + 1, e, l, r, 2 * i + 2);
}
// Function to update the segment tree for a given index
// s --> Starting index of segment tree
// e --> Ending index of segment tree
// index --> Index to be changed in the original array
// diff --> This is to be added in the nodes that contains index in their range
// i --> Current index of Segment tree
void updateValue(int *tree, int s, int e, int index, int diff, int i) {
// If the current node does not contain index in its range, make no changes
if (index < s || index > e)
return;
// Current node contains the index in its range, update the current nodes and its children
// Left child index = 2 * i + 1
// Right child index = 2 * i + 2
tree[i] = tree[i] + diff;
if (s != e) {
int mid = (s + e) / 2;
updateValue(tree, s, mid, index, diff, 2 * i + 1);
updateValue(tree, mid + 1, e, index, diff, 2 * i + 2);
}
}
// A function to create the segment tree recursively between s and e
// i --> Index of current node in the segment tree
int constructSegmentTree(int *tree, int *a, int s, int e, int i) {
// Leaf node case
if (s == e) {
tree[i] = a[s];
return a[s];
}
// For all other nodes its value is sum of left and right child's value
// Left child index = 2 * i + 1
// Right child index = 2 * i + 2
int mid = (s + e) / 2;
tree[i] = constructSegmentTree(tree, a, s, mid, i * 2 + 1) +
constructSegmentTree(tree, a, mid + 1, e, i * 2 + 2);
// Return the value of current node
return tree[i];
}
// Driver function for segment tree approach
int main() {
int a[] = {2, 5, 9, 8, 11, 3};
int n = sizeof(a)/sizeof(a[0]);
// Calculate the size of the segment tree
int x = (int)(ceil(log2(n)));
int size = 2*(int)pow(2, x) - 1;
// Allocate memory for segment tree
int tree[size];
// Construct the segment tree
constructSegmentTree(tree, a, 0, n - 1, 0);
// Queries
int q = 3;
int type[] = {2, 1, 2}; // Stores the type of query to process
int l[] = {3, 2, 0}; // Stores the index of element to be updated for type-1 query and lower range for type-2 query
int r[] = {5, 8, 5}; // Stores the new value of element for type-1 query and higher range for type-2 query
for (int j = 0; j < q; j++) {
if (type[j] == 1) {
// Type-1 query (Update the value of specified index)
int index = l[j];
int value = r[j];
int diff = value - a[index]; // This diff is to be added to all the range that contains the index
// Update the value in array a
a[index] = value;
// Update segment tree
updateValue(tree, 0, n - 1, index, diff, 0);
} else {
// Type-2 query (Find the Sum of given range)
int sum = rangeSum(tree, 0, n - 1, l[j], r[j], 0);
cout<<sum<<endl;
}
}
return 0;
}22 37
Complexity Analysis
The time complexity for the type-1 query is O(1) and for the type-2 query, it is O(n), this can be optimized by the use of a segment tree.