In sorted array to balanced BST problem, we have given an array in sorted order, construct a Balanced Binary Search Tree from the sorted array.
Table of Contents
Examples
Input
arr[] = {1, 2, 3, 4, 5}
Output
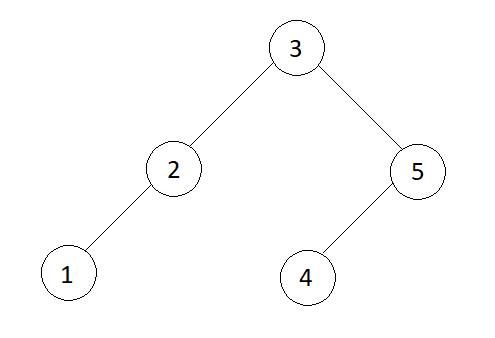
Pre-order : 3 2 1 5 4
Input
arr[] = {7, 11, 13, 20, 22, 41}
Output
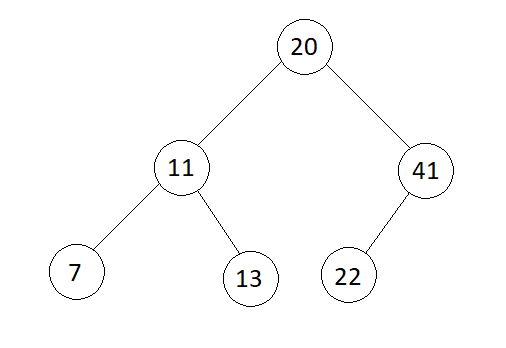
Pre-order : 20 11 7 13 41 22
Algorithm
The in-order traversal of a Binary Search Tree results in sorted data. Here we are given a sorted array and we have to convert it into a Balanced Binary Search Tree.
It can be seen that the middle element of the array forms the root of a balanced binary search tree, and the elements to the left of the array form the left sub-tree of the balanced BST and elements to the right side of the middle element forms the right sub-tree of the balanced BST. Recursively repeating this procedure over the left and right sub-tree will result in a balanced Binary Search Tree.
As in the case of Sorted Linked List to Balanced BST case, we have seen that it takes an O(n) time complexity to find the middle element in the linked list, but in case of the array this complexity reduces to O(1) due to random access property of the array. Hence the naive approach in case of the linked list becomes the optimal approach in case of an array.
- Find the middle element of the array, let its index be mid.
- The element at index mid forms the root of the balanced BST.
- Elements to the left of mid forms the left sub-tree, so recursively call this function for the left sub-tree.
- Elements to the right of mid forms the right sub-tree, so recursively call this function for the right sub-tree also.
- Return root.
Time Complexity = O(n)
Space Complexity = O(n), due to recursion
where n is the size of a given array.
JAVA Code for convert Sorted Array to Balanced BST
public class SortedArrayToBalancedBST {
// class representing node of a binary tree
static class Node {
int data;
Node left, right;
public Node(int data) {
this.data = data;
}
}
// function to print the preorder traversal of a binary tree
private static void preorder(Node root) {
if (root != null) {
System.out.print(root.data + " ");
preorder(root.left);
preorder(root.right);
}
}
private static Node convertSortedArrayToBalancedBST(int[] arr, int start, int end) {
// Base Case
if (start > end) {
return null;
}
// find the middle element of the array
int mid = (start + end) / 2;
// the middle element forms the root of the balanced BST
Node root = new Node(arr[mid]);
// elements to the left of mid forms the left subtree
root.left = convertSortedArrayToBalancedBST(arr, start, mid - 1);
// elements to the right of mid forms the right subtree
root.right = convertSortedArrayToBalancedBST(arr, mid + 1, end);
// return root
return root;
}
public static void main(String[] args) {
// Example 1
int arr1[] = new int[] {1, 2, 3, 4, 5};
Node root1 = convertSortedArrayToBalancedBST(arr1, 0, arr1.length - 1);
preorder(root1);
System.out.println();
// Example 2
int arr2[] = new int[] {7, 11, 13, 20, 22, 41};
Node root2 = convertSortedArrayToBalancedBST(arr2, 0,arr2.length - 1);
preorder(root2);
System.out.println();
}
}3 1 2 4 5 13 7 11 22 20 41
C++ Code for convert Sorted Array to Balanced BST
#include <iostream>
using namespace std;
// class representing node of a binary tree
class Node {
public:
int data;
Node *left;
Node *right;
Node(int d) {
data = d;
left = right = NULL;
}
};
// function to print the preorder traversal of a binary tree
void preOrder(Node *root) {
if (root != NULL) {
cout<<root->data<<" ";
preOrder(root->left);
preOrder(root->right);
}
}
Node* convertSortedArrayToBalancedBST(int *arr, int start, int end) {
// Base Case
if (start > end) {
return NULL;
}
// find the middle element of the array
int mid = (start + end) / 2;
// the middle element forms the root of the balanced BST
Node *root = new Node(arr[mid]);
// elements to the left of mid forms the left subtree
root->left = convertSortedArrayToBalancedBST(arr, start, mid - 1);
// elements to the right of mid forms the right subtree
root->right = convertSortedArrayToBalancedBST(arr, mid + 1, end);
// return root
return root;
}
int main() {
// Example 1
int arr1[] = {1, 2, 3, 4, 5};
Node *root1 = convertSortedArrayToBalancedBST(arr1, 0, sizeof(arr1) / sizeof(arr1[0]) - 1);
preOrder(root1);
cout<<endl;
// Example 2
int arr2[] = {7, 11, 13, 20, 22, 41};
Node *root2 = convertSortedArrayToBalancedBST(arr2, 0, sizeof(arr2) / sizeof(arr2[0]) - 1);
preOrder(root2);
cout<<endl;
return 0;
}3 1 2 4 5 13 7 11 22 20 41