Verify Preorder Serialization of a Binary Tree

Difficulty Level Medium
Frequently asked in Google
Binary Tree Stack TreeViews 2396

First, we need to know what actually Preorder of a Binary Tree is. Preorder is a type of Binary Tree traversal. In this traversal first, we visit the node. After visiting traverse the left sub-tree first and then right sub-tree. Now, move to what we have to do in this problem. We have given an array of string type. Where each string may have “#” which denote the null node or have some numeric value in string format like “123”. We need to find the array of the string given to us is our preorder traversal of any binary tree? If it denotes the preorder of any binary tree then print “YES” else print “NO”.

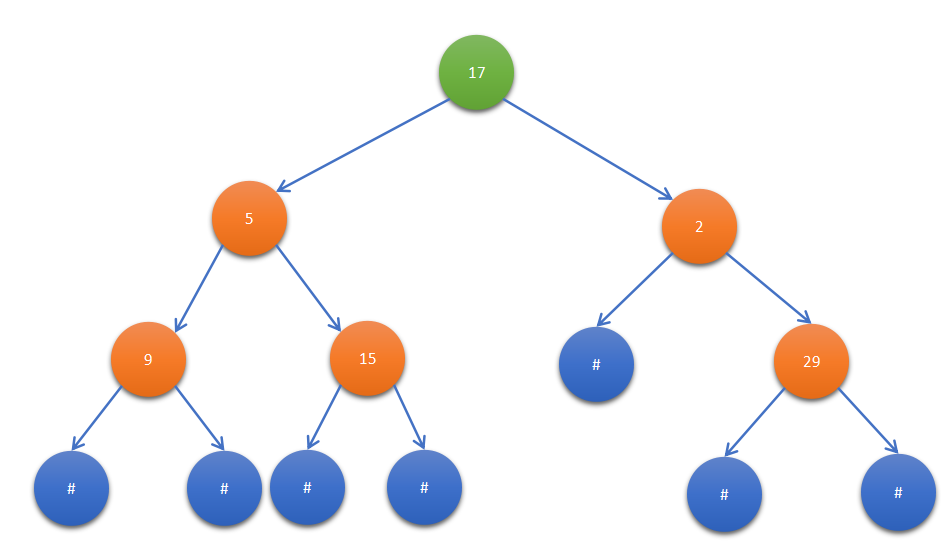
Verify Preorder Serialization of a Binary Tree

If we have given an array { “17”, “5”, “9”, “#”, “#”, “15”, “#”, “#”, “2”, “#”, “29”, “#”, “#”}. We can say the given input is the preorder of above binary tree. So we print “YES” as our output.

Input Format

First-line contain an integer value N which defines the length of the string array.

Second-line contain the input array of string type whose size is N.

Output Format

Print in single-line “YES” if the input array is preorder of any binary tree else print “NO”.

Constraints

  • 1<=N<=100000
  • 1<=|array[i]|<=100000
Sample Input:
13
17 5 9 # # 15 # # 2 # 29 # #
Sample Output:
YES

Explanation: The input array is representing the preorder traversal of the above binary tree.

Here, we just count the total number of “null” node at a particular node[i] and if the null node is greater than (i-count of null nodes) then directly print “NO”.Here 0<=i<=n-1. If we reach the end of the array and don’t the above condition then print “YES” if null node counts equal to i-count of null nodes) else print “NO”. The concept is simple we just check at each node whether our null node is greater than the nodes containing some value.

Verify Preorder Serialization of a Binary Tree

Here we traverse all the null count array and don’t meet the condition null_count[i] > (i-null_count[i]). Then we check at the end null_count[n-1]==(n-1) then print “YES” else print “NO”.

We also see in the above null_count array we just increase the value which depends upon the previous index value. So, we use just one variable to check the above condition.

Algorithm For Verify Preorder Serialization of a Binary Tree

Step:1 For i in range 0 to N-1:
       If arr[i]="#" then:
          null_count++;
       If null_count>i-null_count+2 then:
          print "NO"
Step:2 If null_count = n+1-null_count then:
          print "YES"
       Else:
          print "NO"

Implementation For Verify Preorder Serialization of a Binary Tree

/*C++ Implementation of "Verify Preorder Serialization of a Binary Tree".*/ 
#include<bits/stdc++.h> 
using namespace std; 
int main() 
{
    /*input values.*/
    int n;
    cin>>n;
    string arr[n];
    for(int i=0;i<n;i++)
    {
        cin>>arr[i];
    }
    /*set null count to 0*/
    int null_count=0,flag=0;
    for(int i=0;i<n;i++)
    {
        /*if null node encounter then increase null_count by 1.*/
        if(arr[i]=="#")
        {
            null_count++;
        }
        /*check condition*/
        if(null_count>(i-null_count+2)&&i<n-1)
        {
            flag=1;
            cout<<"NO"<<endl;
            break;
        }
    }
    /*print result*/
    if(flag==0)
    {
        if(null_count==(n-null_count+1))
        {
            cout<<"YES"<<endl;
        }
        else
        {
            cout<<"NO"<<endl;
        }
    }
    return 0;
}
11 
17 5 9 # # 15 # # 2 # #
YES

Time Complexity

O(N) where N is the number of string present in the input array. We just use one loop to count the null nodes and check the condition.

Space Complexity

O(1) because we use only one variable for storing the count of null nodes. The space used for taking input is O(N).

References

Translate ยป