Vertical sum in a given binary tree

Problem Statement

“Vertical sum in a given binary tree” problem states that you are given a binary tree and we need to find the sum of each vertical level. By vertical level, we mean if we draw vertical lines at a distance of 1 unit in the left and right direction then the nodes crossed by ith line are said to be at ith vertical distance.

Example

Input

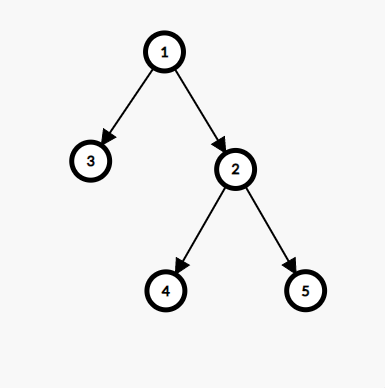
3, 5, 2, 5

Explanation: Node with value 3 is at level -1, and nodes 1 and 4 are at level 0. Thus their sum is 5. Similarly, we solve for nodes at levels 1 and 2. Thus the answer is 3, 5, 3, 5.

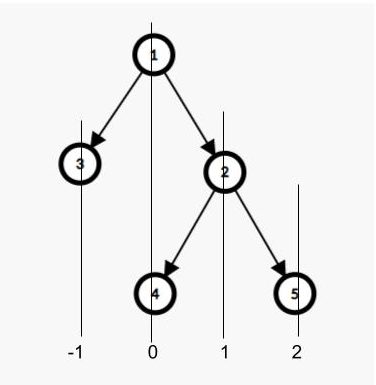
Here the number below the lines denotes the horizontal level of each line.

Approach for Vertical sum in a given binary tree

For solving this problem, we will assign some horizontal level to each of the nodes and we will use a map to store the answer for each horizontal level. Thus, in the end, we have the sum for each level because, in the end, we have traversed all the nodes of the binary tree.

The approach regarding the horizontal distance is simple. We assign 0 to the root, and if we move to the right of the root, we assign 1 and -1 for left. Similarly, for a node at the horizontal level or horizontal distance “h” we assign h-1 to left and h+1 to the right. Now, we will simply traverse the tree and keep on adding the value at each node to the map where the key is the horizontal distance.

Code

C++ code for Vertical sum in a given binary tree

#include<bits/stdc++.h>
using namespace std;

struct node{
    int data;
    node *left;
    node *right;
};

node* create(int data){
    node *tmp = new node();
    tmp->data = data;
    tmp->left = tmp->right = NULL;
}


void fillVerticalSums(node *root,int horizontalLevel,map<int,int> &verticalSums){

    // base case
    if(!root)
        return;
    // recursively call for the left subtree
    fillVerticalSums(root->left, horizontalLevel-1, verticalSums);
    // add the value of current node to the current horizontal distance
    verticalSums[horizontalLevel] += root->data;
    // recursively call for right subtree
    fillVerticalSums(root->right, horizontalLevel+1, verticalSums);
}

void verticalSum(node *root)
{
    // map which stores the sum of nodes at each horizontal level
    map<int, int> verticalSums;
    fillVerticalSums(root, 0, verticalSums);
    // map stores the data in sorted order
    for(auto x: verticalSums)
        cout<<x.second<<" ";
}

int main()
{
    // here we have made a binary tree
    node *root = create(1);
    root->left = create(3);
    root->right = create(2);
    root->right->left = create(4);
    root->right->right = create(5);
    cout<<"The Vertical Sums: ";
    verticalSum(root);

    return 0;
}

The Vertical Sums: 3 5 2 5

Java code for Vertical sum in a given binary tree

import java.util.*;
// Class that denotes a node of the tree
class Node 
{ 
    int data; 
    Node left, right; 
  
    public Node(int data) 
    { 
        this.data = data;
        left = right = null; 
    } 
}

class Tree 
{ 
    static Node root;
  static void fillVerticalSums(Node root, int horizontalLevel, TreeMap<Integer, Integer> verticalSums){
  
      // base case
      if(root == null)
          return;
      // recursively call for the left subtree
      fillVerticalSums(root.left, horizontalLevel-1, verticalSums);
      // add the value of current node to the current horizontal distance
      if(verticalSums.containsKey(horizontalLevel))
      	verticalSums.put(horizontalLevel, verticalSums.get(horizontalLevel) + root.data);
      else
      	verticalSums.put(horizontalLevel, root.data);
      // recursively call for right subtree
      fillVerticalSums(root.right, horizontalLevel+1, verticalSums);
  }

  static void verticalSum(Node root)
  {
      // map which stores the sum of nodes at each horizontal level
      TreeMap<Integer, Integer> verticalSums = new TreeMap<Integer, Integer>();
      fillVerticalSums(root, 0, verticalSums);
      // map stores the data in sorted order
      for(Map.Entry<Integer, Integer> entry: verticalSums.entrySet())
      	System.out.print(entry.getValue()+" ");
  }
  
    public static void main(String args[]) 
    { 
    	// here we have made a binary tree
        Tree tree = new Tree(); 
        tree.root = new Node(1); 
        tree.root.left = new Node(3); 
        tree.root.right = new Node(2); 
        tree.root.right.left = new Node(4); 
        tree.root.right.right = new Node(5); 
  
        System.out.print("The Vertical Sums: ");
        verticalSum(tree.root);
    }
}

The Vertical Sums: 3 5 2 5

Complexity Analysis

Time Complexity

O(N log N)  because we just traversed over the tree that is we traversed over only N nodes. And since the insertion, searching and deletion take log N time per operation. That’s why we have a log N factor.

Space Complexity

O(N) because we have stored only N nodes in the tree.