Table of Contents
What is merge sort?
Merge Sort is a Recursive Procedure. It is also a divide and conquers algorithm. Now we need to know what divide and conquer algorithm is? It’s a type of procedure in which we divide the problem into subproblems and divide them until we find the shortest solved subproblem. By merging the shortest solved subproblem we find the solution to the big/main problem. Let’s see the algorithm for merge_sort.
Algorithm
Step:1 Break the problem into 2 subproblems.
Step:2 Subproblems call recursively till they reach to a minimum size(solved subproblem).
Step:3 Merge the solved subproblems.
Now, move to the example for understanding how this algorithm works?
Explanation For Merge Sort
Let’s take we have an array A containing N number in unsorted. A= {9,1,4,2,5,3,7,2,6,17}
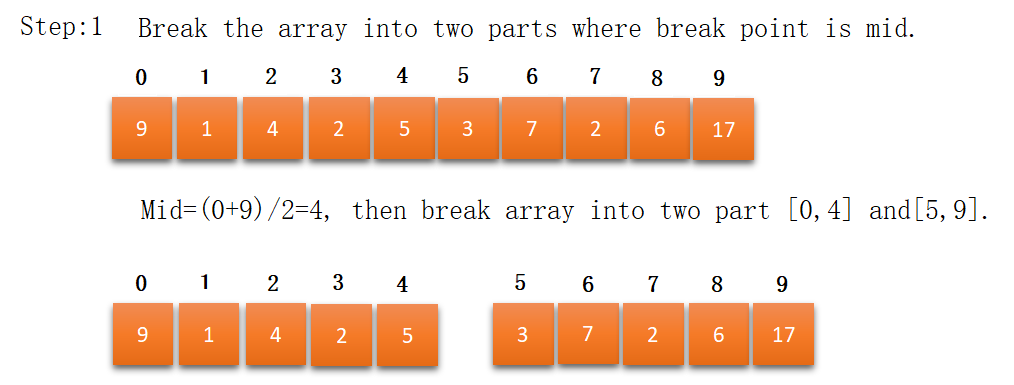
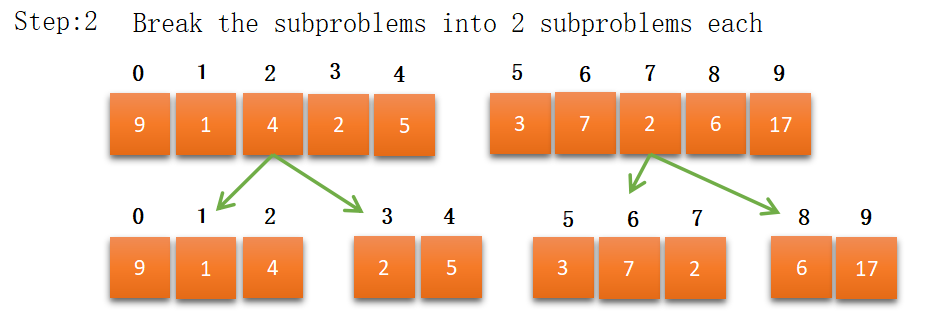
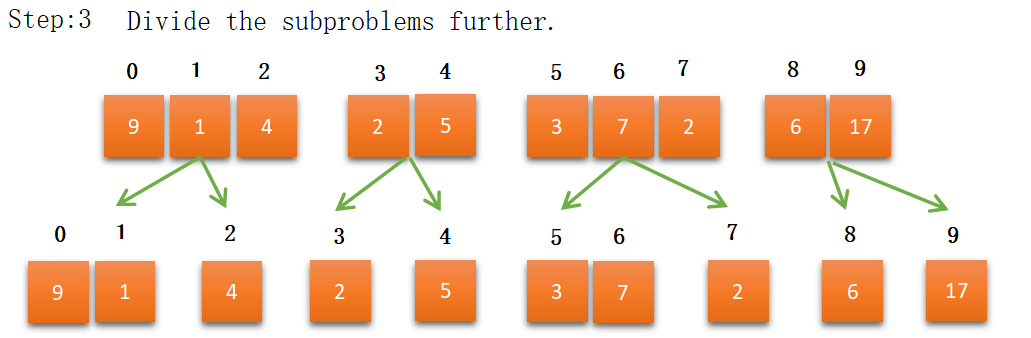
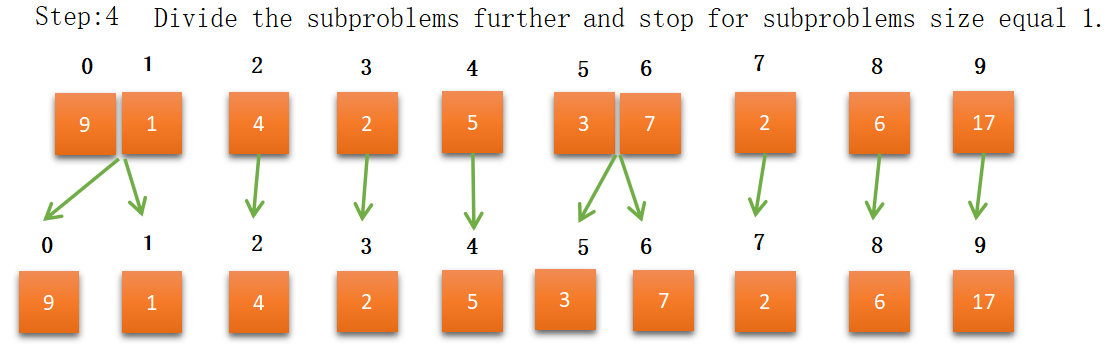




In step 8 we got the final sorted array using the merge_sort algorithm.
Implementation For Merge Sort
/*C++ Implementation of Merge Sort*/
#include<bits/stdc++.h>
#define max_v 100000
using namespace std;
void add_subproblems(int a[],int l,int mid,int r)
{
int start_1=l;//starting index of subproblem 1;
int start_2=mid+1;//strating index of subproblem 2;
int store=l;//used to store the no in array a with O(1) space complexity.
/*compare the element from begining of both subproblems and choose the minimum element from them
and increment the index wrt minimum value by 1.*/
while(start_1<=mid&&start_2<=r)
{
if((a[start_1]%max_v)<=(a[start_2]%max_v))
{
a[store]+=(a[start_1]%max_v)*max_v;
store++;
start_1++;
}
else
{
a[store]+=(a[start_2]%max_v)*max_v;
store++;
start_2++;
}
}
/*if some elements are remaining in subproblem 1*/
while(start_1<=mid)
{
a[store]+=(a[start_1]%max_v)*max_v;
store++;
start_1++;
}
/*if some elements are remaining in subproblem 2*/
while(start_2<=r)
{
a[store]+=(a[start_2]%max_v)*max_v;
store++;
start_2++;
}
/*now change the elements into their oroginal values*/
for(int i=l;i<=r;i++)
{
a[i]/=max_v;
}
}
void merge(int a[],int l,int r)
{
if(l<r)
{
int mid=(l+r)/2;
merge(a,l,mid);
merge(a,mid+1,r);
add_subproblems(a,l,mid,r);
}
}
int main()
{
int number;
/*total numbers which we want to sort*/
cin>>number;
int a[number];
/*take input*/
for(int i=0;i<number;i++)
{
cin>>a[i];
}
cout<<"Array before sorting: ";
/*print the array*/
for(int i=0;i<number;i++)
{
cout<<a[i]<<" ";
}
cout<<"\n";
/*call merge function*/
merge(a,0,number-1);
cout<<"Array after sorting: ";
/*print the array*/
for(int i=0;i<number;i++)
{
cout<<a[i]<<" ";
}
cout<<"\n";
return 0;
}10 9 1 4 2 5 3 7 2 6 17
Array before sorting: 9 1 4 2 5 3 7 2 6 17 Array after sorting: 1 2 2 3 4 5 6 7 9 17
Time complexity
O(N*log N) where N is the total number present in an array. The recurrence relation of the above implementation is T(N)= 2*T(N/2)+O(1).
Space Complexity
O(1) here we did not create any extra space except given array so, the space complexity is O(1) which is constant.
Type of algorithm used
Here we use the divide and conquer approach to solve merge sort.