01 Matrix LeetCode Solution

Difficulty Level Medium
Frequently asked in Adobe Amazon Apple Bloomberg ByteDance Facebook Google Microsoft UberViews 5232

Problem Statement

In this problem 01 Matrix LeetCode Solution, we need to find the distance of the nearest 0 for each cell of the given matrix. The matrix consists only of 0’s and 1’s and the distance of any two adjacent cells is 1.

Examples

Example 1:

01 Matrix LeetCode Solution

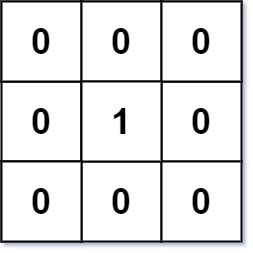
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2:

01 Matrix LeetCode Solution

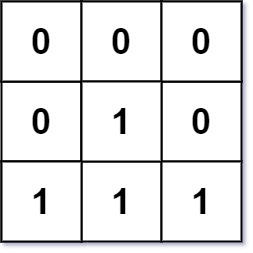
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]

Explanation

consider the matrix mat 0 indexed

  • eg.1: all the cells except mat[1][1] have 0’s and hence distance from these cells to the nearest 0 is 0. The nearest distance from mat[1][1] to 0 is any adjacent cell, i.e 1 unit.
  • eg. 2. cells having value 1 and adjacent cell value 0 has distance 1, cell mat[2][1] is 2 units apart from nearest 0

Approach

This problem can be solved using brute force but it will cause TLE.

The approach discussed below uses Dijkstra’s algorithm having edge weights as 1 unit or modified BFS. There are 2 intuitions for BFS depending on where the distance is being calculated.

  1. We can traverse all the cells, if the cell value is 0, we store 0 otherwise apply BFS on this cell. For this approach, we need to call the BFS function inside the nested loops, and hence time complexity will be high.
  2. We use a queue to store the coordinates of all the cells having a value of 0 and use Dijkstra’salgorithm to calculate the nearest 0. Initially, the distance for each cell having value 0 is 0 and infinity or INT_MAX otherwise. Pop the front element and traverse its neighbors, if the newly calculated distance is smaller, we push its coordinates into the queue and update the distance.

Clearly, the second approach will save us from running BFS inside the nested loops and we can achieve a much faster algorithm using it.

Code

C++ Code for 01 Matrix LeetCode Solution

#define vvi vector<vector<int>>
#define iPair pair<int,int>
class Solution {
    int dir[4][2] = { { -1, 0 }, { 1, 0 }, { 0, -1 }, { 0, 1 } };
    void bfs(queue<iPair> &q, vvi &res, int r, int c) {
         while(!q.empty()) {
            iPair curr = q.front();
            q.pop();
            int x = curr.first, y = curr.second;
            for(auto d:dir) {
                int newX = x+d[0], newY = y+d[1];
                
                if(newX >= 0 && newX < r && newY>=0 && newY < c) {
                    if(res[newX][newY] > res[x][y] + 1) {
                        res[newX][newY] = res[x][y] + 1;
                        q.push({newX,newY});
                    }
                }
            }
        }
    }
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        int r = mat.size(), c = mat[0].size();
        vvi res(r, vector<int> (c,INT_MAX));
        queue<iPair> q;
        for(int i=0; i<r; i++) {
            for(int j=0; j<c; j++) {
                if(!mat[i][j]) {
                    res[i][j] = 0;
                    q.push({i,j});
                }
            }
        }

        bfs(q, res, r, c);       
        return res;
    }
};

Java Code for 01 Matrix LeetCode Solution

class Solution {
    public int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    
    public void bfs(Queue<int[]> q, int[][] matrix, int r, int c) {
        while (!q.isEmpty()) {
            int[] cell = q.poll();
            for (int[] d : dirs) {
                int x = cell[0] + d[0];
                int y = cell[1] + d[1];
                if (x < 0 || x >= r || y < 0 || y >= c || 
                    matrix[x][y] <= matrix[cell[0]][cell[1]] + 1) continue;
                q.add(new int[] {x, y});
                matrix[x][y] = matrix[cell[0]][cell[1]] + 1;
            }
        }
    }
    
    public int[][] updateMatrix(int[][] matrix) {
        int r = matrix.length;
        int c = matrix[0].length;
        
        Queue<int[]> q = new LinkedList<>();
        for (int i = 0; i < r; i++) {
            for (int j = 0; j < c; j++) {
                if (matrix[i][j] == 0) {
                    q.offer(new int[] {i, j});
                }
                else {
                    matrix[i][j] = Integer.MAX_VALUE;
                }
            }
        }
        
        bfs(q, matrix, r, c);
        
        
        
        return matrix;
    }
}

Complexity Analysis for 01 Matrix LeetCode Solution

  • Time complexity: O(r*c)Since the new cells are added to the queue only if their current distance is greater than the calculated distance, cells are not likely to be added multiple times.
  • Space complexity: O(r*c)An additional O(r*c) space is required to maintain the queue.
Translate »