Table of Contents
Problem statement
In the problem “Best Time to Buy and Sell Stock with Cooldown” we are given an array where each element in the array contains the price of the given stock on that day.
There is no restriction on the number of transactions. The definition of the transaction is buying one share of stock and selling that one share of stock.
Our task is to find the maximum profit under the following restrictions:
- we can’t buy a new stock if we have not sold the previous stock. that is at a time we can have at most one stock.
- if we sell a stock on the ith day then we can not buy stock on (i+1)th day. That is 1 day of cooldown period
Example
prices = [1,2,3,0,2]
3
Explanation: maximum profit that can be obtained is 3. Following is the transaction detail:
First day: buy
Second day: sell
Third day: cooldown
Fourth day: buy
Fifth day: sell
Approach for Best Time to Buy and Sell Stock with Cooldown Leetcode Solution
To solve this problem we need to note down a few things:
- Whenever we want to sell a stock we must have bought the stock earlier. Means selling a stock is dependent on buying a stock.
- One day of the cooldown period is a must. So buying a stock is dependent on cooldown period.
Keeping in mind these points we can define the states:
- STATE-A: In this state, we can either buy a stock or just take rest.
- STATE-B: After buying a stock we can either sell the stock or simply take the rest.
- STATE-C: This is a cooldown state. Once the cooldown period is over we move to STATE-A.
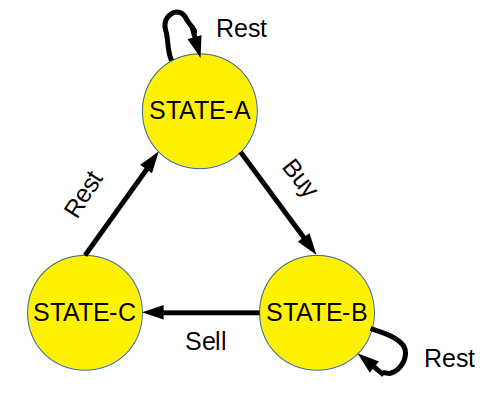
The relationship between these three states can be converted into an algebraic expression where STATE-X[i] represents the maximum profit until the ith day at state x.
sa->STATE-A,sb->STATE-B,sc->STATE-C sa[i]=max(sa[i-1],sc[i-1]); sb[i]=max(sb[i-1],sa[i-1]-prices[i]); sc[i]=sb[i-1]+prices[i];
After n iteration, the maximum profit will be max(sa[n-1], sc[n-1]) because, as we want to maximize the profit so we won’t end up buying a stock and not selling it.
Base cases:
sa[0]=0; sb[0]=-prices[0] sc[0]=INT_MIN
Implementation
C++ code for Best Time to Buy and Sell Stock with Cooldown
#include <bits/stdc++.h>
using namespace std;
int maxProfit(vector<int>& prices) {
int n=prices.size();
if(n<1)return 0;
int sa[n],sb[n],sc[n];
sa[0]=0,sb[0]=-prices[0],sc[0]=INT_MIN;
for(int i=1;i<n;i++)
{
sa[i]=max(sa[i-1],sc[i-1]);
sb[i]=max(sb[i-1],sa[i-1]-prices[i]);
sc[i]=sb[i-1]+prices[i];
}
return max(sa[n-1],sc[n-1]);
}
int main()
{
vector<int> arr = { 1,2,3,0,2 };
cout<<maxProfit(arr)<<endl;
return 0;
}3
Java code for Best Time to Buy and Sell Stock with Cooldown
import java.util.Arrays;
public class Tutorialcup {
public static int maxProfit(int[] prices) {
int n=prices.length;
if(n<1)return 0;
int[] sa = new int[n];
int[] sb = new int[n];
int[] sc = new int[n];
sa[0] = 0;sb[0] = -prices[0]; sc[0] = Integer.MIN_VALUE;
for (int i = 1; i < n; ++i) {
sa[i] = Math.max(sa[i-1],sc[i-1]);
sb[i] = Math.max(sb[i-1],sa[i-1]-prices[i]);
sc[i] = sb[i-1]+prices[i];
}
return Math.max(sa[n-1],sc[n-1]);
}
public static void main(String[] args) {
int [] arr = {1,2,3,0,2};
int ans= maxProfit(arr);
System.out.println(ans);
}
}3
Complexity Analysis of Best Time to Buy and Sell Stock with Cooldown Leetcode Solution
Time complexity
The time complexity of the above code is O(n) because we are traversing the price array only once. Here n is the length of the price array.
Space complexity
The space complexity of the above code is O(n) because we using an array to store information of different states.