Binary Tree Maximum Path Sum LeetCode Solution

Difficulty Level Hard
Frequently asked in Adobe Amazon Apple Bloomberg ByteDance DiDi DoorDash Facebook Flipkart Google LinkedIn Microsoft Myntra Oracle Paytm Samsung Snapchat Sprinklr Twitter Uber VMware Wish Yahoo Yandex
Shopee tiktok TuSimple Walmart Global techViews 3529

Problem Statement

Binary Tree Maximum Path Sum LeetCode Solution – A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node’s values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

Example

Test Case 1:

Input:

root = [-10, 9, 20, null, null, 15, 7]

Binary Tree Maximum Path Sum LeetCode Solution

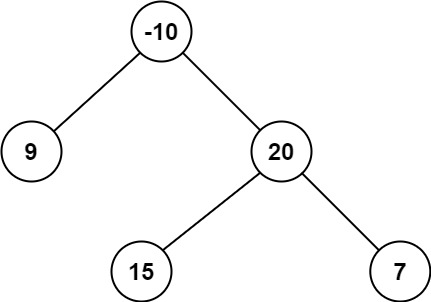
Output:

42

Explanation

The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42 .

Binary Tree Maximum Path Sum LeetCode Solution

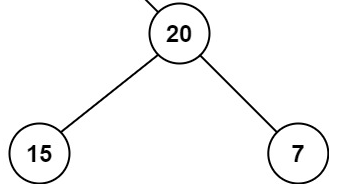
Approach:

The idea behind this problem is the following:

  • For every node of the tree, find the max among : leftSum, rightSum, root.val, leftSum + root.val , rightSum + root.val, leftSum + rightSum + root.val
  • Save the max to the global max
  • Now, you can’t return the global max. You need to return the max of leftSum + root.val, rightSum + root.val or root.val. This ensures that you are looking at a contiguous series of nodes.

The idea is also DFS. From bottom to up, at every node, we have four choices:

  1. the left sub-path ==> node ==> the right sub-path.
  2. the left sub-path ==> node ==> upper. The left sub-path may yield a negative sum, in which case we set node->left sub-path to zero.
  3. the right sub-path ==> node ==>upper. The right sub-path may yield a negative sum, in which case we set node->right sub-path to zero.
  4. 0 ==> upper, which means we abandon the entire tree rooted at this node because of a negative-sum.

Noted: Negative node values are possible.

Code for Binary Tree Maximum Path Sum

C++ Program

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    int maxPathSum(TreeNode *root, int &ma)
    {
        if (!root)
            return 0;
        int left =  maxPathSum(root->left, ma);
        int right = maxPathSum(root->right, ma);
        ma = max(ma, root->val + left + right);
        return max(max(0, max(left, right)) + root->val, 0);
    }

public:
    int maxPathSum(TreeNode* root)
    {
        if (!root)
            return INT_MIN;  //This INT_MIN is just to comply with the judge.
        
        int ma = root->val;
        
        maxPathSum(root, ma);
        
        return ma;
    }
};

Java Program

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int maxSum = Integer.MIN_VALUE;
    public int maxPathSum(TreeNode root) {
        dfs(root);
        return maxSum;
    }
    
    public int dfs(TreeNode node) {
        if (node == null) return 0;
        
        int left = Math.max(dfs(node.left), 0);
        int right = Math.max(dfs(node.right), 0);
        
        maxSum = Math.max(maxSum, node.val + left + right);
        return node.val + Math.max(left, right);
    }
}

Complexity Analysis for Binary Tree Maximum Path Sum LeetCode Solution

Time Complexity: O(N)

Space Complexity: O(H)

Translate »