Cells with Odd Values in a Matrix LeetCode Solution

Problem Statement

Cells with Odd Values in a Matrix LeetCode Solution –  There is an m x n matrix that is initialized to all 0‘s. There is also a 2D array indices where each indices[i] = [r_i, c_i] represents a 0-indexed location to perform some increment operations on the matrix.

For each location indices[i], we need to do both of the following:

1. Increment all the cells on row r_i.
2. Increment all the cells on the column c_i.

Given m, n, and indices, return the number of odd-valued cells in the matrix after applying the increment to all locations in indices.

Input: m = 2, n = 3, indices = [[0,1],[1,1]]
Output: 6
Explanation: Initial matrix = [[0,0,0],[0,0,0]].
After applying first increment it becomes [[1,2,1],[0,1,0]].
The final matrix is [[1,3,1],[1,3,1]], which contains 6

odd numbers

.

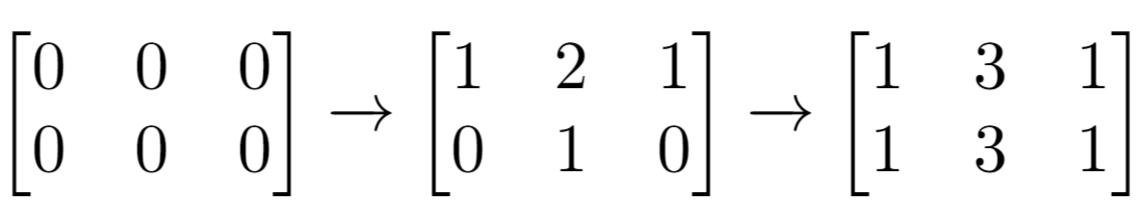
Explanation

A brute-force approach that also gets accepted due to low constraints in the question is to traverse for every row-col pair in indices and increment the matrix.
Finally, calculate the odd valued numbers.
This approach will take  : O (i * (m+n)) time with O(m*n) space

We are going to discuss an optimized solution in the article, so let’s move to that.

Intuition

Each time a row or a column is encountered in the indices array it gets incremented, so if that row/column is a there an odd number of times in the indices array then the result of that row/column will be odd.

Two things to note here are:

1. if x rows are odd and y columns are odd the x*y elements will become even as they will be common in both row and col. (So we need to subtract them : x*y) 
2. If x rows are odd then x*n elements will be counted and if y columns are odd then y*m elements will be counted but due to this elements with row=column will be counted twice (so we need to subtract them: -x*y)

So now then final equation will be :

Ans  : odd_row * n + odd_col * m – 2 * odd_row * odd_col

The above equation can further be simplified to: odd_row * even_col + odd_col * even_row

HOW ??

(Replace n with : odd_col + even_col and m with : odd_row+even_row )

Now the only task left is to get odd rows and odd columns. For this, we will use the Bitwise XOR operator. Which you can see in the code.

Code

Java Program for Cells with Odd Values in a Matrix LeetCode Solution

class Solution {
    public int oddCells(int n, int m, int[][] indices) {
      boolean[] oddRows = new boolean[n], oddCols = new boolean[m];
      int cntRow = 0, cntCol = 0;
      for (int[] idx : indices) {
          oddRows[idx[0]] ^= true;
          oddCols[idx[1]] ^= true;
      }
      for (boolean r : oddRows)
          cntRow += r ? 1 : 0;
      for (boolean c : oddCols)
          cntCol += c ? 1 : 0;
      // return m * cntRow + n * cntCol - 2 * cntRow * cntCol;
      return (m - cntCol) * cntRow + (n - cntRow) * cntCol;
  }
}

C++ Program for Cells with Odd Values in a Matrix LeetCode Solution

class Solution {
public:
    int oddCells(int n, int m, vector<vector<int>>& indices) {
        vector<bool> N(n, false);
        vector<bool> M(m, false);
        
        for(int i=0; i<indices.size(); i++) {
            N[indices[i][0]] = N[indices[i][0]]^true;
            M[indices[i][1]] = M[indices[i][1]]^true;
        }
        
        int r = 0;
        int c = 0;
        
        for(int i=0; i<n; i++) {
            if(N[i])
                r++;
        }
        
        for(int j=0; j<m; j++) {
            if(M[j])
                c++;
        }
        
        return  r*m + c*n - 2*r*c;
    }
};

Python Program for Cells with Odd Values in a Matrix LeetCode Solution

class Solution:
    def oddCells(self, n: int, m: int, indices: List[List[int]]) -> int:
            odd_rows, odd_cols = [False] * n, [False] * m
            for r, c in indices:
                odd_rows[r] ^= True
                odd_cols[c] ^= True
            # return m * sum(odd_rows) + n * sum(odd_cols) - 2 * sum(odd_rows) * sum(odd_cols)
            return (m - sum(odd_cols)) * sum(odd_rows) + (n - sum(odd_rows))* sum(odd_cols)

Complexity Analysis for Cells with Odd Values in a Matrix LeetCode Solution

Time Complexity

Time: O(L + m + n)

Space Complexity

space: O(m + n), where L = indices.length.