Closest Binary Search Tree Value II LeetCode Solution

Difficulty Level Hard
Frequently asked in Amazon Google LinkedIn OracleViews 1928

Problem Statement:

Closest Binary Search Tree Value II LeetCode Solution: Given the root of a binary search tree, a target value, and an integer k, return the k values in the BST that are closest to the target. You may return the answer in any order.

You are guaranteed to have only one unique set of k values in the BST that are closest to the target.

Examples:

Input:

 root = [4,2,5,1,3], target = 3.714286, k = 2

Output:

 [4,3]

Approach:

Idea:

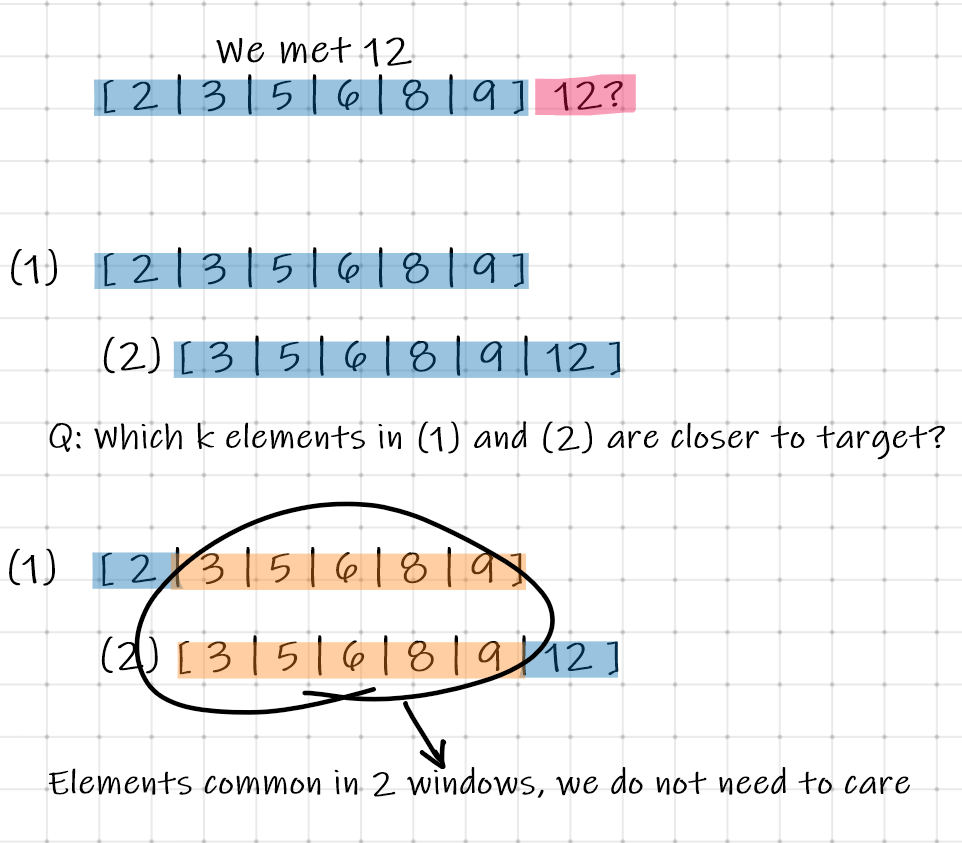
The problem can be solved by traversing over the tree using any of the traversals. While traversing, we will push the element and its absolute difference with the target value into a maxheap, ensuring that at no time the heap size is greater than k. The idea is to create a heap based on the absolute difference. Once the traversal is done we will simply pop off all the elements from the maxheap into a list.

Basically, we want to make sure that, Whenever we remove from res, it should the element with largest difference with the target among those k elements. It’s somehow achieving the purpose without Priority Queue. Let’s see how:

If we use a priority queue, we are not using the property that this binary tree is a BST too. The solution with a priority queue will work on a binary tree, not just BST. Since we have BST here, we can traverse the elements in an ordered manner, specifically in increasing order if we do in-order traversal. This property allows us to use a normal queue instead of a special priority queue.

Closest Binary Search Tree Value II LeetCode Solution

Code:

Closest Binary Search Tree Value II C++ Solution:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorder;
    priority_queue<pair<double,int>> maxheap;

    void inOrder(TreeNode* root,double target, int k){
        if(!root)
            return;
        inOrder(root->left,target,k);
        maxheap.push({abs(root->val-target),root->val});
        if(maxheap.size()>k)
            maxheap.pop();
        inOrder(root->right,target,k);
    }
    
    vector<int> closestKValues(TreeNode* root, double target, int k) {
        inOrder(root,target,k);
        
        vector<int> ans;
        while(!maxheap.empty()){
            ans.push_back(maxheap.top().second);
            maxheap.pop();
        }
        return ans;
    }
};

Complexity Analysis of Closest Binary Search Tree Value II LeetCode Solution:

  • Time complexity: The time complexity of the above code is to push n elements into the heap of the size k.
  • Space complexity: The space complexity of the above code is to keep the heap of k elements and the recursion stack of the tree height h.
Translate »