Count Good Nodes in Binary Tree Leetcode Solution

Table of Contents

Problem Statement

In this problem a binary tree is given with its root. A node X in the tree is named good if in the path from root to X there are no nodes with a value greater than X.

We have to return the number of good nodes in the given binary tree.

Example

Explanation:

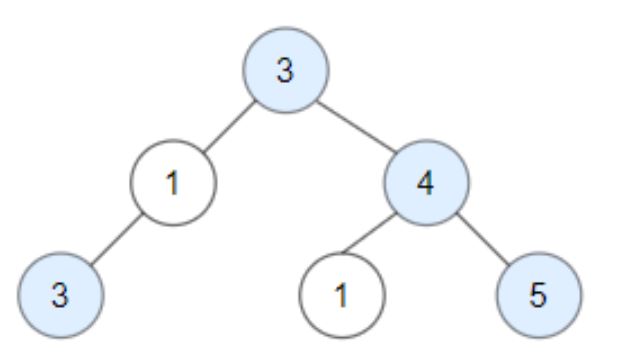
Nodes in blue are good.
Root Node (3) is always a good node.
Node 4 -> (3,4) is the maximum value in the path starting from the root.
Node 5 -> (3,4,5) is the maximum value in the path
And Node 3 -> (3,1,3) is the maximum value in the path.

Explanation:

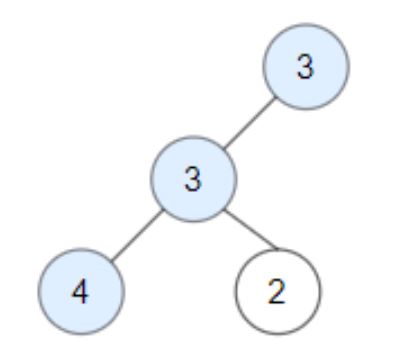
Node 2 -> (3, 3, 2) is not good, because “3” is higher than it.

Approach

To find whether a node is good or not we must traverse path from root to the that node and check if its value is not smaller than maximum in this path.
To find the number of good nodes we have to check like this for each node of the given binary tree. But here observe one thing,

if we find the answer for a particular node by traversing its path from root, we can go to its child node also from there itself because we have already traversed almost path of child node also and we also have maximum value traversed till yet. We just have to update the maximum with current node value to transfer to its both children node.
So this looks like a DFS or recursion where to go to a particular node we traverse the path from root to that node. Thus in this problem recursion will be very helpful. The steps are:

Create a recursive function with two arguments as its parameter. One is the address of the node and second is the maximum value we found till here.
Now whenever we will be at a particular node we will check if current node value is smaller than current max. If it is not smaller we will add this node to our ans and call the same function for its child nodes after updating the maximum value.

Implementation

C++ Program for Count Good Nodes in Binary Tree Leetcode Solution

#include <bits/stdc++.h>
using namespace std;

struct TreeNode {
    int val;
    TreeNode *left,*right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

int rec(TreeNode* root, int mx)
{
   if(!root) return 0;

    int cur=0;
    if(mx <= root->val) cur++;

    mx=max(mx,root->val);
    return rec(root->left,mx) + rec(root->right,mx) + cur;
}

int goodNodes(TreeNode* root) {

    int mx= INT_MIN;
    return rec(root,mx);
}

int main() 
{
    TreeNode* root= new TreeNode(3);
    root->left=  new TreeNode(1);
    root->right=  new TreeNode(4);
    root->left->left=  new TreeNode(3);
    root->right->left=  new TreeNode(1);
    root->right->right=  new TreeNode(5);
    
    cout<< goodNodes(root) ;
    return 0; 
}

Java Program for Count Good Nodes in Binary Tree Leetcode Solution

class Rextester{
    
static class TreeNode {
    int val;
    TreeNode left,right;
    TreeNode(int x)  {
        val=x;
        left=null;
        right=null;
    }
}
    
    static int rec(TreeNode root, int mx)
    {
        if(root==null) return 0;
        
        int cur=0;
        if(mx <= root.val) cur++;
        
        mx = Math.max(mx,root.val);
        return rec(root.left,mx) + rec(root.right,mx) + cur;
    }
    
    public static int goodNodes(TreeNode root) 
    {     
        int mx= Integer.MIN_VALUE;
        return rec(root,mx);       
    }
    
  public static void main(String args[])
    {
        TreeNode root= new TreeNode(3);
        root.left=  new TreeNode(1);
        root.right=  new TreeNode(4);
        root.left.left=  new TreeNode(3);
        root.right.left=  new TreeNode(1);
        root.right.right=  new TreeNode(5);
        
        System.out.println( goodNodes(root) );
    }
}

Complexity Analysis for Count Good Nodes in Binary Tree Leetcode Solution

Time Complexity

O(n) : where n is the total number of nodes in the given binary tree. We are visiting each node once.

Space Complexity

O(n) : Space used will be the maximum size of recursion stack. At worst it can go to O(n) size in case of skewed binary tree.