Table of Contents
Problem statement
In the problem “Count Negative Numbers in a Sorted Matrix” we are given a matrix of n rows and m columns. Elements are sorted in decreasing order both row-wise and column-wise. We need to find the total number of negative elements in the matrix.
Example
grid = [[8,3,2,-1],[4,2,1,-1],[3,1,-1,-2],[-1,-1,-2,-3]]
8
Explanation: As in the given matrix negative numbers are: {-1,-1,-1,-2,-1,-1,-2,-3}. So the total count of the negative numbers is 8.
Approach
To understand the approach better let us use the same example for better understanding. We will see the given matrix as a set of positive and negative values and will ignore its magnitude. So the given matrix is converted into a set of positive and negative values.
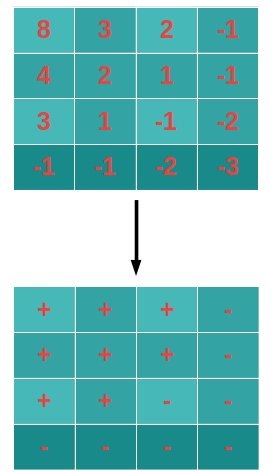
So we already know that the matrix is sorted in decreasing order row-wise as well as column-wise, we will use it to solve this problem. We will start with the first row and will start traversing from right to left until we encounter a positive element(let’s call it col). The total number of negative elements in the first row will be => m – col – 1. Now we will jump to the next row. Here comes the use of the fact that elements are sorted. We need not traverse elements that are to the left of the col because the value of matrix[0][col]>=matrix[1][col] and all elements right to the matrix[1][col] is smaller than it.
Now if matrix[1][col] is positive then The total number of negative elements in the first row will be => m – col – 1 else we will keep traversing from right to left until we encounter a positive element. We will follow these steps until we visit all the rows. The final total count of negative numbers from all the rows will be our answer.
Code
C++ code for Count Negative Numbers in a Sorted Matrix LeetCode Solution
#include <bits/stdc++.h>
using namespace std;
int count(vector<vector<int>>& grid)
{
int n=grid.size(),m=grid[0].size(), row=0, column=m - 1,ans=0;
while (row < n) {
while (column >= 0 && grid[row][column] < 0) column--;
ans += m - column - 1;
row++;
}
return ans;
}
int main()
{
vector<vector<int> > arr = { { 8,3,2,-1 },
{ 4,2,1,-1 },
{ 3,1,-1,-2 },
{ -1,-1,-2,-3 }};
cout<<count(arr)<<endl;
return 0;
}8
Java code for Count Negative Numbers in a Sorted Matrix LeetCode Solution
public class Tutorialcup {
public static int countNegatives(int[][] grid) {
int n=grid.length,m=grid[0].length, row=0, column=m - 1,ans=0;
while (row < n) {
while (column >= 0 && grid[row][column] < 0) column--;
ans += m - column - 1;
row++;
}
return ans;
}
public static void main(String[] args) {
int [][] grid = {
{8,3,2,-1},
{4,2,1,-1},
{3,1,-1,2},
{-1,-1-2,-3}
};
int ans= countNegatives(grid);
System.out.println(ans);
}
}
8
Complexity Analysis
Time complexity
The time complexity of the above code is O(n+m) because we are traversing each row and at worst case all columns. Here n and m are the numbers of rows and number of columns respectively.
Space complexity
The space complexity of the above code is O(1) because we are using only a variable to store answer.