Count Odd Numbers in an Interval Range Leetcode Solution

Difficulty Level Easy
Frequently asked in Microsoft
algorithms coding Interview interviewprep LeetCode LeetCodeSolutions MathViews 6725

Problem Statement

In this problem, we are given two non-negative integers low and high. We have to find how many odd numbers are there in the given interval range [ low, high ].

Example

low = 3, high = 7
3

Explanation:

The odd numbers between 3 and 7 are [3, 5, 7].

low = 8, high = 10
1

Explanation:

The odd numbers between 8 and 10 are [9].

Approach

One way to find the total count of odd numbers in the given interval range is to traverse from the left to right boundary of the interval in a loop and increase the odd counter for each odd number. But this will be a very lame approach for counting odd numbers in a range. This will take linear time complexity, and that we don’t want for such an easy problem.

It is very easy to find total odd numbers in the given interval range as we know there are almost half even and half odd numbers in an interval range.
But we have to consider the interval boundaries very carefully. So what we can do is we can form the formula for the count of odd numbers in first n natural numbers. Let it be count[n]. Then odd numbers between low and high will be equal to :
count[ low, high ] = count[high] – count[low-1].

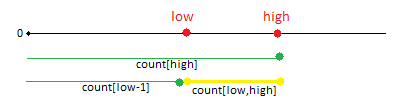
Count Odd Numbers in an Interval Range Leetcode Solution

Now taking some examples for count[i] :

count[1]=1
count[2]=1
count[3]=2
count[4]=2
count[5]=3

We can deduce that count[n] = (n+1)/2
Hence count[ low , high ] = (high+1)/2 – low/2

Implementation

C++ Program (Naive Approach) for Count Odd Numbers in an Interval Range Leetcode Solution

#include <iostream>
using namespace std;

int countOdds(int low, int high) 
{
    int count=0;
    for(int i=low;i<=high;i++)
        if(i%2==1) count++;
        
    return count;
}

int main()
{
    int low=3,high=7;  
    cout<< countOdds(low, high) <<endl;
}
3

Java Program (Naive Approach) for Count Odd Numbers in an Interval Range Leetcode Solution

class CountOdd
{  
    public static int countOdds(int low, int high) 
    {
        int count=0;
        for(int i=low;i<=high;i++)
            if(i%2==1) count++;
        
        return count;
    }
    
    public static void main(String args[])
    {
        int low=3,high=7;
        System.out.println(countOdds(low, high));
    }
}
3

C++ Program (Optimum Approach)

#include <iostream>
using namespace std;

int countOdds(int low, int high) 
{
   return (high + 1) / 2 - low / 2;       
}

int main()
{
    int low=3,high=7;  
    cout<< countOdds(low, high) <<endl;
}
3

Java Program (Optimum Approach)

class CountOdd
{  
    public static int countOdds(int low, int high) 
    {
        return (high + 1) / 2 - low / 2;   
    }
    
    public static void main(String args[])
    {
        int low=3,high=7;
        System.out.println(countOdds(low, high));
    }
}
3

Complexity Analysis for Count Odd Numbers in an Interval Range Leetcode Solution

Time Complexity

Traversing for each number will take O(n) time complexity while calculating the ans using formula takes constant time O(1) to execute.

Space Complexity 

O(1): No extra space is used in both the solutions except a variable that is used to store the ans.

Translate »