Table of Contents
Problem Statement
In this problem, we are keep tracking of our position in a folder system. We are initially at the root folder or the main folder of this system.
We have basically 3 kind of commands here. The commands are in the form of string in which each string means a command.
- “../” means go to the parent folder of the current folder (if already in the root folder then don’t go anywhere).
- “./” stay in the current folder.
- “x/” go into the child folder of the current folder which has name x.
We are given a sequence of commands which is a combination of above 3 commands. We have to find out the minimum number of operation to go back to the root folder after preforming the given commands.
e.g.
logs = [“d1/”,”d2/”,”../”,”d21/”,”./”]
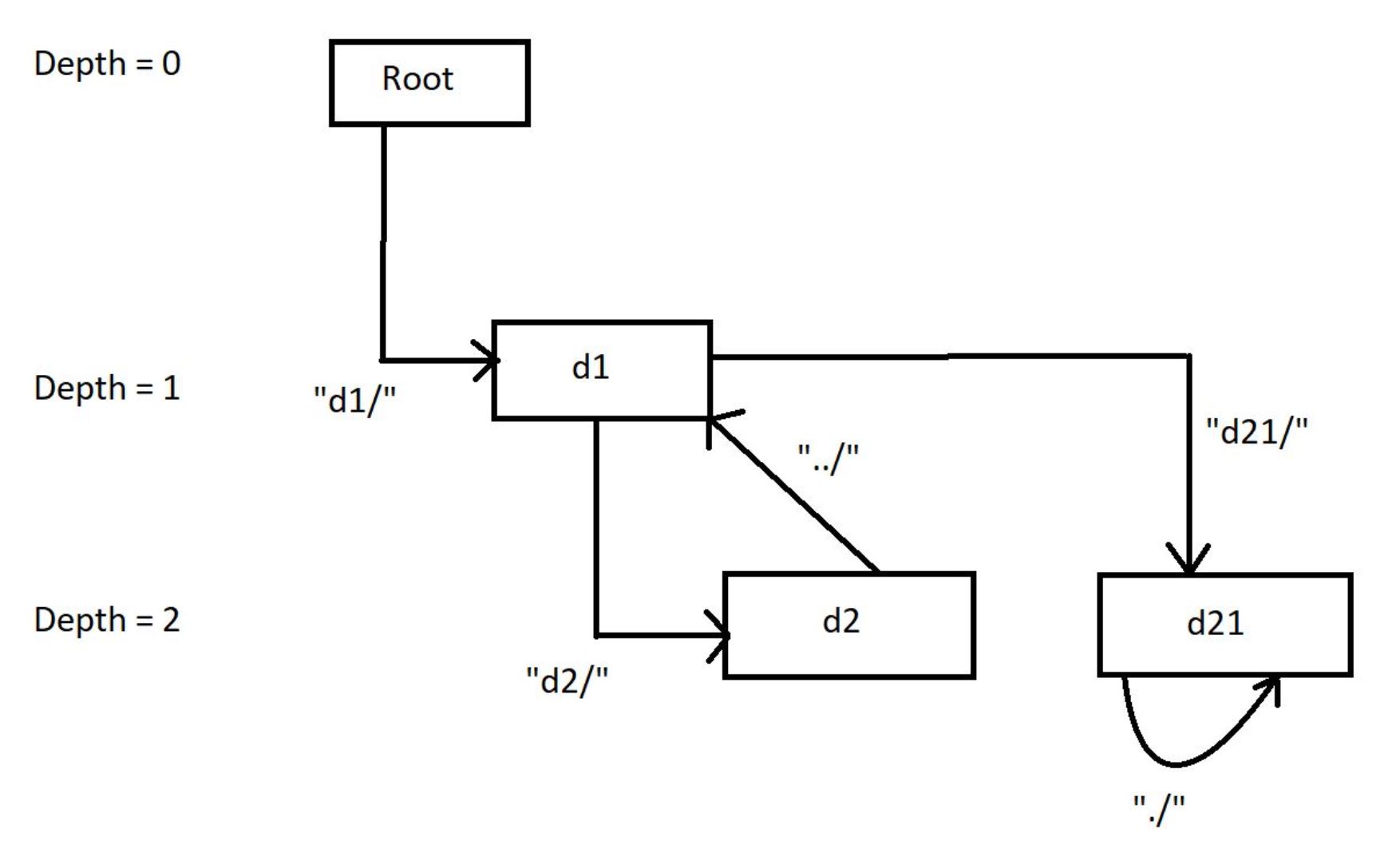
We are at the depth 2 from the root folder. Hence, our answer will be 2.
Example
logs = ["d1/","d2/","../","d21/","./"]
2
Explanation:
Use this change folder operation “../” 2 times and go back to the main folder.
logs = ["d1/","d2/","./","d3/","../","d31/"]
3
Approach 1 (Using Stack)
We can use a stack of file names. Initially our stack is empty. Whenever we have to move to a subfolder then the name of the subfolder is pushed into the stack. Thus, the folder in which we are currently present will always remain on the top of the stack.
So, whenever we encounter “../”, means we have to come out of the current folder (i.e. move to parent folder), then we will check if the current folder is root. If no, then we will pop the top element from stack.
And of course whenever we will encounter a “./”, we have to do nothing.
We are handling these three cases using if else if ladder.
One thing we should know here that the number of element present in the stack is saying that at what depth we are currently from root folder.
Thus, we will return size of stack in the end i.e. depth from root folder.
Implementation for Crawler Log Folder Leetcode Solution
C++ Program
#include <iostream>
#include <stack>
#include <vector>
using namespace std;
int minOperations(vector<string>& logs) {
stack<string>stack;
for(string log:logs){
if(log=="../"){
if(stack.size()>0)stack.pop();
}
else if(log=="./");
else{
stack.push(log);
}
}
return stack.size();
}
int main()
{
vector<string>logs{"d1/","d2/","../","d21/","./"};
cout<<minOperations(logs);
}
2
Java Program
import java.util.*;
import java.lang.*;
class Solution
{
public static int minOperations(String[] logs) {
Stack<String>stack=new Stack<String>();
for(String log:logs){
if(log.equals("../")){
if(stack.size()>0)stack.pop();
}
else if(log.equals("./"));
else{
stack.push(log);
}
}
return stack.size();
}
public static void main(String args[])
{
String[]logs={"d1/","d2/","../","d21/","./"};
System.out.println(minOperations(logs));
}
}2
Complexity Analysis for Crawler Log Folder Leetcode Solution
Time Complexity
O(n): We are traversing the given array of strings linearly and doing stack operation in O(1) time in each iteration. Thus, time complexity is O(n), where n is length of input array.
Space Complexity
O(n): We have used a stack whose size can be equal to given input array length. Thus, the worst case space complexity is O(n).
Approach 2 (Using a depth variable)
The problem can be easily solved by just keep tracking a depth variable which is basically showing that at what depth we are from root folder.
Each time we are going to a child folder, we are going far from the root folder by distance 1.( i.e. depth++ )
Each time we are going to a parent folder, we are decreasing coming nearer to root folder by distance 1. (i.e. depth–).
Note that we can only move to parent folder if we are not in the root folder.
So, we will start executing the commands from left to right in a for loop .
- If we will encounter “../” we will check if we are in root folder or not. If no then we will decrease depth by 1.
- Else if we will encounter “./” we have to stay in current folder, thus no change in depth variable.
- Else we have to move to one of our child folder. Thus, we will increase our depth by 1.
After all the commands, our depth variable is storing the distance from the root folder. We will return it as output.
Implementation for Crawler Log Folder Leetcode Solution
C++ Program
#include <iostream>
#include <vector>
using namespace std;
int minOperations(vector<string>& logs)
{
int depth=0;
for(string log:logs)
{
if(log=="../")
{
if(depth>0)depth--;//moving to parent folder only if depth>0 i.e. current folder is
other than main folder
}
else if(log=="./"); //staying to current folder
else depth++; //moving to child folder
}
return depth;
}
int main()
{
vector<string>logs{"d1/","d2/","../","d21/","./"};
cout<<minOperations(logs);
}2
Java Program for Crawler Log Folder Leetcode Solution
import java.util.*;
import java.lang.*;
class Solution
{
public static int minOperations(String[] logs)
{
int depth=0;
for(String log:logs)
{
if(log.equals("../"))
{
if(depth>0)depth--;//moving to parent folder only if depth>0 i.e. current folder is other than main folder
}
else if(log.equals("./")); //staying to current folder
else depth++; //moving to child folder
}
return depth;
}
public static void main(String args[])
{
String[]logs={"d1/","d2/","../","d21/","./"};
System.out.println(minOperations(logs));
}
}2
Complexity Analysis for Crawler Log Folder Leetcode Solution
Time Complexity
O(n): We are executing all the commands once. Thus, time complexity is O(n).
Space Complexity
O(1): we have just used a depth variable. Thus, space complexity is O(1).