Decompress Run-Length Encoded List Leetcode Solution

Difficulty Level Easy
Frequently asked in Amazon Apple Google
algorithms Array coding Interview interviewprep LeetCode LeetCodeSolutionsViews 3418

The problem Decompress Run-Length Encoded List Leetcode Solution states that you are given an array or vector containing a sequence. The sequence has some specific representation. The input sequence is formed from another sequence. We will call that another sequence as the original sequence. As per which the input sequence has been created. We are asked to find the original sequence. Each odd (ith) index in the sequence represents the number of times the following (i+1th) index is repeated in the original sequence. So, as always before diving into the solution let’s take a look at a few examples.

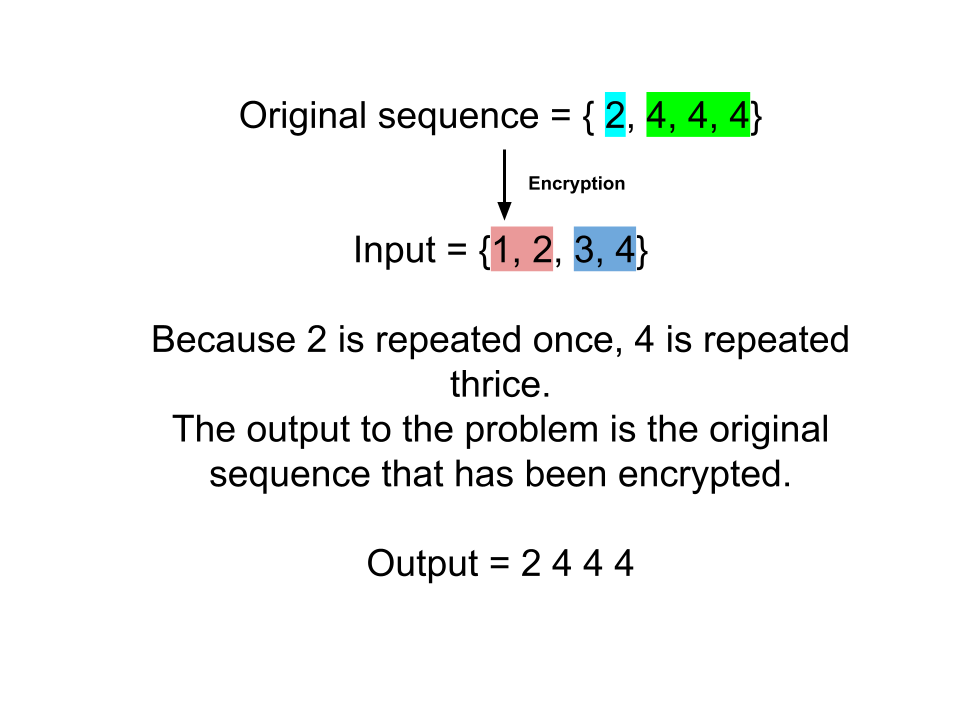
Decompress Run-Length Encoded List Leetcode Solution

nums = [1,2,3,4]
[2,4,4,4]

Explanation: Let us verify if the output is correct? 2 is repeated 1 time in the original statement. So in the input sequence, it should be 1, 2. Afterward, 4 is repeated 3 times, which is also shown in the input sequence So, this proves that the output is correct.

nums = [1,1,2,3]
[1,3,3]

Explanation: Again if we verify the output. 1 has a single copy and 3 is repeated twice. Once again the output is correct.

Approach for Decompress Run-Length Encoded List Leetcode Solution

The problem Decompress Run-Length Encoded List Leetcode Solution is a standard one. And is asked frequently in several coding rounds conducted by various companies. The approach is very simple since we need to create a new array to store the original sequence. We simply use either array or a vector and keep on adding elements in the back.

We can run a for loop that jumps 2 units after each iteration. This confirms that we deal only with (frequency, value) pairs. Now again with a nested for loop, we add the element at the ith index to vector. We run the nested for loop as per the element at i+1th index in the given input sequence.

Code for Decompress Run-Length Encoded List Leetcode Solution

C++ code

#include <bits/stdc++.h>
using namespace std;

vector<int> decompressRLElist(vector<int>& nums) {
    vector<int> tmp;
    for(int i=0;i<nums.size();i+=2){
        for(int j=0;j<nums[i];j++)
            tmp.push_back(nums[i+1]);
    }
    return tmp;
}

int main(){
    vector<int> input = {1,2,3,4};
    vector<int> output = decompressRLElist(input);
    for(auto x: output)cout<<x<<" ";
}

2 4 4 4

Java code

import java.util.*;
import java.lang.*;
import java.io.*;

class Main
{
  public static int[] decompressRLElist(int[] nums) {
        int size = 0, k = 0;
        for(int i=0;i<nums.length;i+=2)
            size += nums[i];
        int[] tmp = new int[size];
        for(int i=0;i<nums.length;i+=2){
            for(int j=0;j<nums[i];j++)
                tmp[k++] = nums[i+1];
        }
        return tmp;
    }
    
  public static void main (String[] args) throws java.lang.Exception{
    int[] input = {1,2,3,4};
      int[] output = decompressRLElist(input);
      for(Integer x: output)System.out.print(x+" ");
  }
}
2 4 4 4

Complexity Analysis

Time Complexity

O(N), where N is the length of the output. Here the time complexity does not depends on the input. Instead of input, the time complexity is dependent on the output or result obtained.

Space Complexity

O(N), where N is the length of the output. Since we store the output because we are returning it. Space is also occupied by it.

Translate »