Table of Contents
Problem Statement :
The Diameter of N-Ary Tree LeetCode Solution – Given a root of an N-ary tree, you need to compute the length of the diameter of the tree.
The diameter of an N-ary tree is the length of the longest path between any two nodes in the tree. This path may or may not pass through the root.
(Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value.)
Example :
Example 1
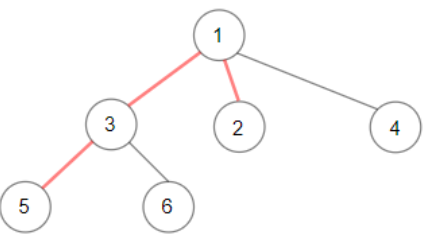
Input: root = [1,null,3,2,4,null,5,6] Output: 3 Explanation: Diameter is shown in red color.
Example 2
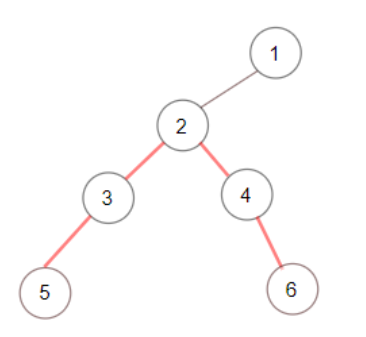
Input: root = [1,null,2,null,3,4,null,5,null,6] Output: 4
Example 3
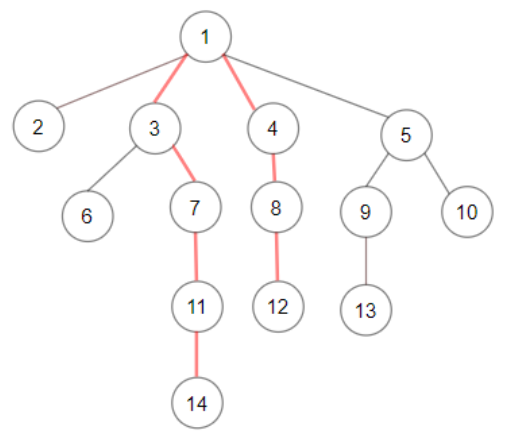
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] Output: 7
Intuition :
- We are asked to calculate the diameter of an N-ary tree, which is defined as the longest path between any two nodes in the tree.
- Consider a node with n children, then there are nC2 or n Choose 2 paths passing through this node.
- The longest path will be given by maxheight1 + maxheight2 +2 where maxheight1 and maxheight2 are the two maximum heights between N children.
- Length of the longest path passing through a node = 1st Max Height among N children + 2nd Max Height among N children + 2
- With the above intuition, to find the diameter of the tree, we need to iterate over all the nodes and select the two children with the maximum height.
- To iterate over all the nodes, we can use Depth-First Search.
Algorithm :
- Initialize a global variable diameter, and for each node update the variable, computing the length of the longest path passing through the node.
- Define a function height(node root) {} that will return the max height.
- In the height function, Iterate over all children and pick the best two children’s height i.e. maxheight1 and maxheight2.
- Now, update the diameter global variable with the longest path passing through this node.
- At last return maxheight1 in the height function.
- After the execution of the height function, return the diameter global variable, in the main function diameter(Node root){}.
Code
Diameter of N-Ary Tree Leetcode Java Solution:
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> children;
public Node() {
children = new ArrayList<Node>();
}
public Node(int _val) {
val = _val;
children = new ArrayList<Node>();
}
public Node(int _val,ArrayList<Node> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
protected int diameter=0;
public int diameter(Node root) {
height(root);
return this.diameter;
}
// Return the maxheight in N-arry tree
public int height(Node root){
int maxheight1=0;
int maxheight2=0;
for(Node child:root.children){
int height=height(child)+1;
if(height>maxheight1){
maxheight2=maxheight1;
maxheight1=height;
}
else if(height>maxheight2){
maxheight2=height;
}
}
this.diameter=Math.max(maxheight1+maxheight2,this.diameter);
return maxheight1;
}
}Diameter of N-Ary Tree Leetcode C++ Solution:
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
int maxDiameter=0;
public:
int diameter(Node* root) {
height(root);
return this->maxDiameter;
}
int height(Node* root){
int maxheight1=0;
int maxheight2=0;
for(auto child:root->children){
int rootHeight=height(child)+1;
if(rootHeight>maxheight1){
maxheight2=maxheight1;
maxheight1=rootHeight;
}
else if(rootHeight>maxheight2){
maxheight2=rootHeight;
}
}
this->maxDiameter=max(maxheight1+maxheight2,this->maxDiameter);
return maxheight1;
}
};Complexity Analysis For Diameter of N-Ary Tree :
Time Complexity
O(N), since we are iterating each node in the tree once and only once via recursion.
O(N), as recursion stack 0(N) is used.