Different Ways to Add Parentheses Leetcode Solution

Problem Statement

The Different Ways to Add Parentheses LeetCode Solution – “Different Ways to Add Parentheses” states that given a string expression of numbers and operators. We need to return all possible results from computing all different possible ways to group numbers and operators.

Return the answer in any order.

Example:

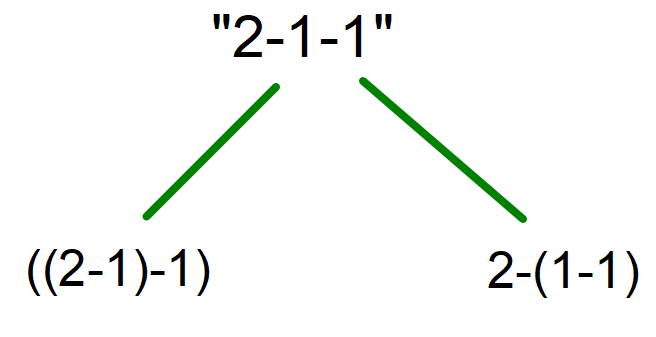
Input:  expression = "2-1-1"

Output: [0,2]

Explanation:

• ((2-1)-1) = 0, is one of the possible result.
• (2-(1-1)) = 2, is also one of the possible result.

Input:  expression = "2*3-4*5"

Output: [-34,-14,-10,-10,10]

Explanation:

• (2*(3-(4*5))) = -34
• ((2*3)-(4*5)) = -14
• ((2*(3-4))*5) = -10
• (2*((3-4)*5)) = -10
• (((2*3)-4)*5) = 10
• Hence, [-34, -14, -10, -10, 10] are the possible results.

Approach

Idea:

1. The main idea to solve this problem is to use Recursion.
2. At every step of the recursion, we have left and right ends of the expression which we need to work on.
3. Iterate for each index i in the range [l,r] and again, recurse for [l,i-1] and [i+1,r]  provided the current character is an operator, and store the set of answers returned in the left and right vector named respectively.
4. Now, for each evaluated expression on the left and right vectors respectively, find all new values after applying the result a op b, where a is an operand in the left, b is an operand in right and op is the operator.
5. Return the answer for the current state {l,r};
6. We can also memoize the result using dynamic programming.

Code

Different Ways to Add Parentheses Leetcode C++ Solution:

class Solution {
public:
    map<pair<int,int>,vector<int>> dp;
    vector<int> solve(int l,int r,string expression){
        if(dp.count({l,r})){
            return dp[{l,r}];
        }
        vector<int> ans;
        for(int i=l;i<=r;i++){
            if(expression[i]=='+' or expression[i]=='-' or expression[i]=='*'){
                vector<int> left = solve(l,i-1,expression);
                vector<int> right = solve(i+1,r,expression);
                
                for(auto& num1:left){
                    for(auto& num2:right){
                        if(expression[i]=='+'){
                            ans.push_back(num1+num2);
                        }
                        else if(expression[i]=='-'){
                            ans.push_back(num1-num2);
                        }
                        else{
                            ans.push_back(num1*num2);
                        }
                    }
                }
            }
        }
        if(ans.empty()){
            ans.push_back(stoi(expression.substr(l,r-l+1)));
        }
        return dp[{l,r}] = ans;
    }
    vector<int> diffWaysToCompute(string expression) {
        return solve(0,expression.length()-1,expression);
    }
};

Different Ways to Add Parentheses Leetcode Java Solution:

public class Solution {
    public List<Integer> diffWaysToCompute(String input) {
        List<Integer> ret = new LinkedList<Integer>();
        for (int i=0; i<input.length(); i++) {
            if (input.charAt(i) == '-' ||
                input.charAt(i) == '*' ||
                input.charAt(i) == '+' ) {
                String part1 = input.substring(0, i);
                String part2 = input.substring(i+1);
                List<Integer> part1Ret = diffWaysToCompute(part1);
                List<Integer> part2Ret = diffWaysToCompute(part2);
                for (Integer p1 :   part1Ret) {
                    for (Integer p2 :   part2Ret) {
                        int c = 0;
                        switch (input.charAt(i)) {
                            case '+': c = p1+p2;
                                break;
                            case '-': c = p1-p2;
                                break;
                            case '*': c = p1*p2;
                                break;
                        }
                        ret.add(c);
                    }
                }
            }
        }
        if (ret.size() == 0) {
            ret.add(Integer.valueOf(input));
        }
        return ret;
    }
}

Complexity Analysis for Different Ways to Add Parentheses Leetcode Solution

Time Complexity

The time complexity of the above code is Catalan Number. For every state [l,r], we are iterating in the range [l,r] and dividing it into two sets [l,i-1] and [i+1,r] which is inversely equal to computing Catalan number. Hence, the time complexity is the same as that of the Catalan numbers.

Space Complexity

The space complexity of the above code is O(answer size).