Table of Contents
Problem Statement
In this problem Find All Possible Recipes from Given Supplies LeetCode Solution, we are required to find the recipes that can be made using the supplies given as a vector of strings. We are also given the recipes we need to make and their corresponding ingredients required.
Examples and Explanation for Find All Possible Recipes from Given Supplies LeetCode Solution
Example 1:
Input: recipes = ["bread"], ingredients = [["yeast","flour"]], supplies = ["yeast","flour","corn"] Output: ["bread"] Explanation: We can create "bread" since we have the ingredients "yeast" and "flour".
Example 2:
Input: recipes = ["bread","sandwich"], ingredients = [["yeast","flour"],["bread","meat"]], supplies = ["yeast","flour","meat"] Output: ["bread","sandwich"] Explanation: We can create "bread" since we have the ingredients "yeast" and "flour". We can create "sandwich" since we have the ingredient "meat" and can create the ingredient "bread".
Example 3:
Input: recipes = ["bread","sandwich","burger"], ingredients = [["yeast","flour"],["bread","meat"],["sandwich","meat","bread"]], supplies = ["yeast","flour","meat"] Output: ["bread","sandwich","burger"] Explanation: We can create "bread" since we have the ingredients "yeast" and "flour". We can create "sandwich" since we have the ingredient "meat" and can create the ingredient "bread". We can create "burger" since we have the ingredient "meat" and can create the ingredients "bread" and "sandwich".
Approach
This problem is very similar to the course scheduling problem on leetcode. This solution uses Kahn’s algorithm for topoSort on the graph of ingredients directed to their corresponding recipes i.e. all the ingredients required for a recipe will be directed towards that recipe. Once, the graph is constructed we can easily print the strings using topoSort and return the topoSort excluding the ingredients.
The picture below depicts the example 3 graph along with the in-degrees of nodes
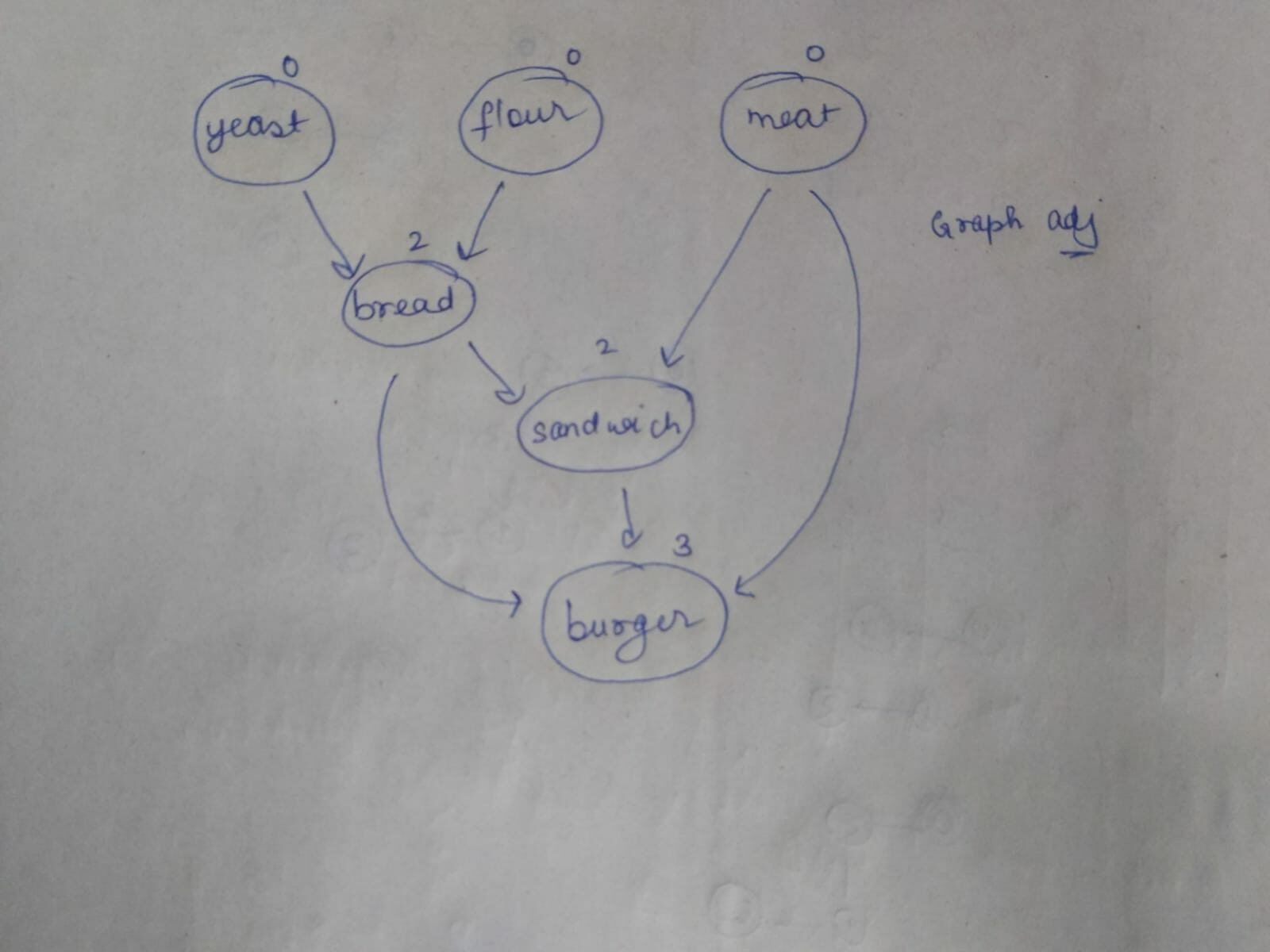
Observations
- all supplies will have an in-degree as 0
- once the recipe[i] can be prepared, we treat it as a supply and hence push recipe[i] into the queue
- keep a map to check what recipes we need to make and only store recipes as answer not ingredients
Code
C++ program for Find All Possible Recipes from Given Supplies
class Solution {
map<string, vector<string>> adj;
map<string, int> indegree;
map<string, int> recipesAvl;
vector<string> res;
public:
vector<string> findAllRecipes(vector<string>& recipes, vector<vector<string>>& ingredients, vector<string>& supplies) {
int n = recipes.size();
for(int i=0; i<n; i++) {
for(int j=0; j<ingredients[i].size(); j++) {
adj[ingredients[i][j]].push_back(recipes[i]);
indegree[recipes[i]]++;
recipesAvl[recipes[i]]=1;
}
}
// to print the graph
// for(auto it:adj) {
// cout<<it.first<<"--->";
// for(auto itr:it.second) cout<<"->"<<itr;
// cout<<"\n";
// }
queue<string> q;
for(string s: supplies) q.push(s);
while(!q.empty()) {
string u = q.front();
q.pop();
// cout<<u<<" ";
if(recipesAvl[u]) {
res.push_back(u);
}
for(string v: adj[u]) {
if(--indegree[v]==0) {
q.push(v);
}
}
}
// cout<<"\n";
return res;
}
};Java program for Find All Possible Recipes from Given Supplies
class Solution {
public List<String> findAllRecipes(String[] recipes, List<List<String>> ingredients, String[] supplies) {
Map<String, ArrayList<String>> adj = new HashMap();
Map<String, Integer> indegree = new HashMap();
Map<String, Integer> recipesAvl = new HashMap();
ArrayList<String> res = new ArrayList();
int n = recipes.length;
for(int i=0; i<n; i++) {
for(int j=0; j<ingredients.get(i).size(); j++) {
String elem = ingredients.get(i).get(j);
if(!adj.containsKey(elem)) {
adj.put(elem, new ArrayList<String>());
}
adj.get(elem).add(recipes[i]);
indegree.put(recipes[i], indegree.getOrDefault(recipes[i], 0) + 1);
recipesAvl.put(recipes[i], 1);
}
}
Queue<String> q = new LinkedList();
for(String s: supplies) q.add(s);
while(!q.isEmpty()) {
String u = q.peek();
q.remove();
if(recipesAvl.containsKey(u)) {
res.add(u);
}
for(String v: adj.getOrDefault(u, new ArrayList<String>())) {
indegree.put(v, indegree.get(v)-1);
if(indegree.get(v)==0) {
q.add(v);
}
}
}
return res;
}
}
Complexity Analysis for Find All Possible Recipes from Given Supplies LeetCode Solution
Let V = number of vertices and E = number of edges in the graph adj
- Time Complexity: O(V+E). The outer for loop will be executed V number of times and the inner for loop will be executed E number of times.
- Auxiliary Space: O(V). The queue and maps need to store all the vertices of the graph So the space required is O(V)