Find if Path Exists in Graph Leetcode Solution

Problem Statement

Find if Path Exists in Graph Leetcode Solution – There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [u_i, v_i] denotes a bi-directional edge between vertex u_i and vertex v_i. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

You want to determine if there is a valid path that exists from the vertex source to vertex destination.

Given edges and the integers n, source, and destination, return true if there is a valid path from source to destination, or false otherwise.

Example

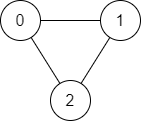
Input:

 n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2

Output:

 true

Explanation:

 There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2

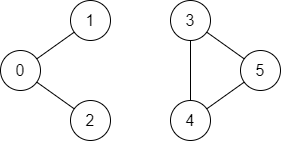
Input:

 n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5

Output:

 false

Explanation:

 There is no path from vertex 0 to vertex 5.

Approach

• This is the most basic problem for learning graph searching.
• You can use either DFS or BFS. BFS is more suitable when you need the shortest path and it’s also more complex to code compared to DFS. So let’s use DFS for this problem
• In DFS we traverse from a start node and go down as deep as possible until either we hit our target node or the end of the path.
• For traversal, we need an adjacency list or matrix, the former being more space-efficient, so let’s use that. Used edges to build adjacency list.
• Start searching from start node and stop when you hit end or have exhausted all paths and not found the target node
• Maintain a visited node-set so that you don’t start traversing from the same node again

Idea:

The main idea is to use the DSU data structure to union the nodes and then we can easily find out whether the source or destination are connected or not by the find method of DSU.

If the source and destination are connected their parents will be the same.

Code

C++ code

class Solution {
public:
    int find(int x,vector<int> &par){
        if(par[x]==-1){
            return x;
        }
        return par[x] = find(par[x],par);
    }
    void unionSet(int x,int y,vector<int> &par,vector<int> &rank){
        int s1 = find(x,par);
        int s2 = find(y,par);
        if(s1!=s2){
            if(rank[s1] > rank[s2]){
                par[s2] = s1;
                rank[s1] += rank[s2];
            }
            else{
                par[s1] = s2;
                rank[s2] += rank[s1];
            }
        }
    }
    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        vector<int> par(n,-1);
        vector<int> rank(n,1);
        
        for(int i=0;i<edges.size();i++){
            int x = edges[i][0];
            int y = edges[i][1];
            unionSet(x,y,par,rank);
            //taking the union of both the nodes x and y means connecting them.
        }
        
        int s1 = find(source,par);
        //finding the parent of source node.
        
        int s2 = find(destination,par);
        //finding the parent of destination node.
        
        return s1==s2;
        //if both source and destination have same parent means they are connected.
        
    }
};

Java Code

class DisjointSetUnion{
    private int[] parent;
    private int[] rank;
    private int N;
    
    public DisjointSetUnion(int n){
        this.N = n;
        this.parent = new int[this.N];
        this.rank = new int[this.N];
        for(int i = 0; i < this.N; i++){
            this.parent[i] = i;
            this.rank[i] = 1;
        }
    }
    
    public boolean areConnected(int u, int v){
        return find(u) == find(v);
    }
    
    public void union(int u, int v){
        if(u != v){
            int a = find(u);
            int b = find(v);
            if(a != b){
                if(rank[a] > rank[b]){
                    parent[b] = a;
                    rank[a] += rank[b];
                }else{
                    parent[a] = b;
                    rank[b] += rank[a];
                }
            }
        }
    }
    
    private int find(int u){
        int x = u;
        while(x != this.parent[x]){
            x = this.parent[x];
        }
        
        this.parent[u] = x;
        return x;
    }
}

class Solution {
    public boolean validPath(int n, int[][] edges, int start, int end) {
        DisjointSetUnion set = new DisjointSetUnion(n);
        for(int[] edge : edges){
            set.union(edge[0], edge[1]);
        }
        
        return set.areConnected(start, end);
    }
}

Complexity Analysis for Find if Path Exists in Graph Leetcode Solution

Time complexity

The time complexity on an average of find and union methods in DSU after applying path compression and union by rank techniques respectively is O(n), So the overall time complexity is O(n).

Space Complexity

The space complexity is O(n) as used by the parent and rank array.