Find the Town Judge Leetcode Solution

Problem Statement

In this problem, we are given n people labelled from 1 to n. We are also given a 2d array trust[][] shows that trust[i][0]th people trusts trust[i][1]th people for each 0 <= i < trust.length.
We have to find a person “town judge” who does not trust any other people and all other people trust him. If no such person exist then return -1 else return the town judge.

Example

#1

N = 2, trust = [[1,2]]

2

#2

N = 3, trust = [[1,3],[2,3],[3,1]]

-1

#3

N = 4, trust = [[1,3],[1,4],[2,3],[2,4],[4,3]]

3

Approach

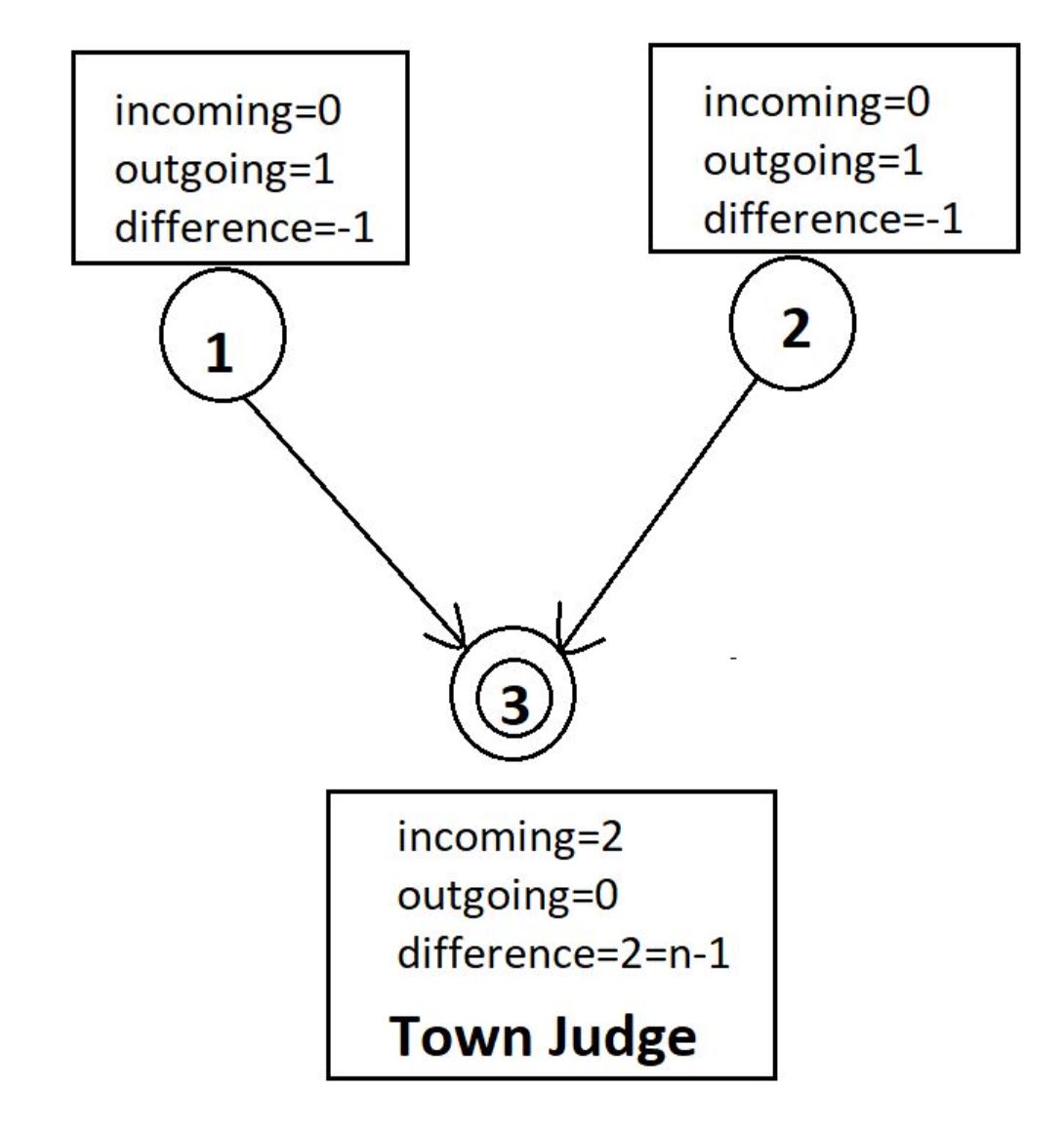
Let’s treat the given scenario as a directed graph in which an edge from person a to b shows that a trusts b.
A town judge does not trust anybody thus, town judge has no outgoing edge. All other n-1 persons trust town judge thus, total n-1 incoming edge towards town judge from all other person.
We can further understand that difference between number of incoming edges and number of outgoing edges is n-1 for town judge only.
If we talk about a simple person then he will surely trust town judge thus min(outgoing edges)=1 and in best case even if all other person trust him(of course town judge won’t trust him) thus max(incoming edges)= n-2.
The maximum difference between incoming and outgoing edges for this person is n-2-(1) = n-3.
Also if there is no town judge then no person can achieve the n-1 difference between number of incoming and outgoing edges.

Now, our main task is to calculate the difference i.e. number of incoming edges – number of outgoing edges for each person. We will do so by traversing the trust array row-wise.
In any row, there are two elements. Left element is who trusts and right element is whom the left element trusts.
Thus left element has outgoing edge to right element. Hence, difference value for left element will decrease by 1 and for right element, increase by 1.
In our code, we have used netTrustGains array for this task. Each index i of this array shows the difference value for ith person.

After traversing trust array, we will run a loop for each person from 1 to n and check if any person has the difference value = n-1.
If such a person is found then we will return him else we will return -1.

Implementation

C++ Program for Find the Town Judge Leetcode Solution

#include <bits/stdc++.h>
using namespace std;
int findJudge(int n, vector<vector<int>>& trust) 
{
    int netTrustGains[n+1];
    memset(netTrustGains, 0, sizeof(netTrustGains));
    for(vector<int>i:trust){
        netTrustGains[i[0]]--;
        netTrustGains[i[1]]++;

    }
    int judge=-1;
    for(int i=1;i<=n;i++){
        if(netTrustGains[i]==n-1){
            judge=i;
        }
    }
    return judge;
}
int main()
{
    int n=3;
    vector<vector<int>>trust
    {
        {1, 3},
        {2, 3}
    };
    cout << findJudge(3,trust);
}

3

Java Program for Find the Town Judge Leetcode Solution

import java.util.*;
import java.lang.*;

class Solution
{  
    public static void main(String args[])
    {
        int n = 3;
        int[][]trust = {{1,3},{2,3}};
        System.out.println(findJudge(n,trust));
    }
    public static int findJudge(int n, int[][] trust) 
    {
        int[]netTrustGains=new int[n+1];
        for(int[]i:trust){
            netTrustGains[i[0]]--;
            netTrustGains[i[1]]++;
            
        }
        int judge=-1;
        for(int i=1;i<=n;i++){
            if(netTrustGains[i]==n-1){
                judge=i;
            }
        }
        return judge;
    }
}

3

Complexity Analysis for Find the Town Judge Leetcode Solution

Time Complexity

O(max(n,trust.size())) : We have traversed the trust loop linearly and another loop is of size n to check the netTrustGains for each person from 1 to n.

Space Complexity 

O(n) : We have created an array netTrustGains of size n+1 thus space complexity O(n).