Graph Valid Tree LeetCode Solution

Difficulty Level Medium
Frequently asked in Amazon Bloomberg Coupang Facebook Google LinkedIn Microsoft Qualtrics Zenefits
TuSimpleViews 3647

Problem Statement

Graph Valid Tree LeetCode Solution – Given the edges of a graph, check if the edges make up a valid tree. If yes, return true and false otherwise. The edges are given as a 2D array of size n*2

Examples & Explanations

Example 1:

Graph Valid Tree LeetCode Solution

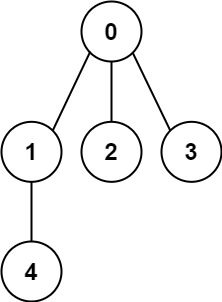
Input: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
Output: true
Explanation: Since it does not conatain any cycle and all

components are connected

, it's a valid tree

Example 2:

Graph Valid Tree LeetCode Solution

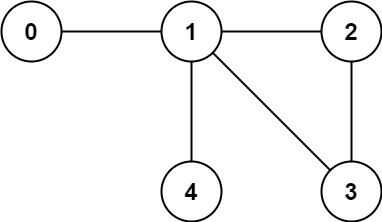
Input: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
Output: false
Explanation: False, because there exists a cycle

Approach

A graph is a valid tree iff

  • does not consist of disconnected components
  • does not have a cycle

Algorithm

We will build the graph using a map and edges (2D array given as input). Check for any cycle present in the graph using DFS/BFS. We will mark the visited node as 1 and if we encounter the same node by traversing via its neighbors at some later point during processing, it means the graph contains a cycle.

Next, we will check if the graph contains any disconnected components. For this, we can check if any node remains unvisited. If there exists, it implies there are disconnected components.

Code

C++ Code for Graph Valid Tree

class Solution {
    bool isCyclic(map<int, vector<int>> &adj, vector<int>&vis, int v, int u) {
        if(vis[v]) return 1;
        vis[v]=1;
        for(int neighbor:adj[v]) {
            if(neighbor != u && isCyclic(adj, vis, neighbor, v)) 
                return 1;
        }
        return 0;
    }
public:
    bool validTree(int n, vector<vector<int>>& edges) {
        // contruct graph using map
        map<int, vector<int>> adj;
        for(auto &edge: edges) {
            adj[edge[0]].push_back(edge[1]);
            adj[edge[1]].push_back(edge[0]);
        }
        
        vector<int> vis(n,0);
        
        if(isCyclic(adj, vis, 0, -1))
            return 0;
        
        for(int i=0; i<n; i++) {
            if(!vis[i])
                return 0;
        }
        
        return 1;
    }
};

Java Code for Graph Valid Tree

class Solution {
    private List<List<Integer>> adj = new ArrayList<>();
    private Set<Integer> vis = new HashSet<>();
    
    boolean dfs(int node, int parent) {
        if (vis.contains(node)) return false;
        vis.add(node);
        for (int neighbour : adj.get(node)) {
            if (parent != neighbour) {
                boolean result = dfs(neighbour, node);
                if (!result) return false;
            }
        }
        return true;
    }
    
    public boolean validTree(int n, int[][] edges) {
        
        if (edges.length != n - 1) return false;
        
        for (int i = 0; i < n; i++)
            adj.add(new ArrayList<>());
        
        for (int[] edge : edges) {
            adj.get(edge[0]).add(edge[1]);
            adj.get(edge[1]).add(edge[0]);
        }

        return dfs(0, -1) && vis.size() == n;   
    }

}

Complexity Analysis for Graph Valid Tree LeetCode Solution

Let E be the number of edges, and N be the number of nodes.

  • Time Complexity: O(N + E)Creating the adjacency list of N nodes and E edges will take  O(E) + O(N) = O(N+E) time. As each node is added to the data structure only once, there will be N iterations and for each node, its adjacent edges will be traversed only once. We are ensuring this by keeping a visited array. Therefore, total E edges are iterated over once by the loop, and hence, the time complexity is O(N + E).
  • Space Complexity: O(N + E)The adjacency list consists of N nodes with E edges, hence O(N + E) space. In the worst case, the stack/ queue will have all N nodes on it at the same time, resulting in a total of O(N) space. Hence the space complexity is O(E + N).
Translate »