Jump Game IV LeetCode Solution

Table of Contents

Problem Statement:

Jump Game IV LeetCode Solution says – Given an array of integers arr, you are initially positioned at the first index of the array.

In one step you can jump from the index i to index:

i + 1 where: i + 1 < arr.length.
i - 1 where: i - 1 >= 0.
j where: arr[i] == arr[j] and i != j.

Return the minimum number of steps to reach the last index of the array.

Notice that you can not jump outside of the array at any time.

Examples:

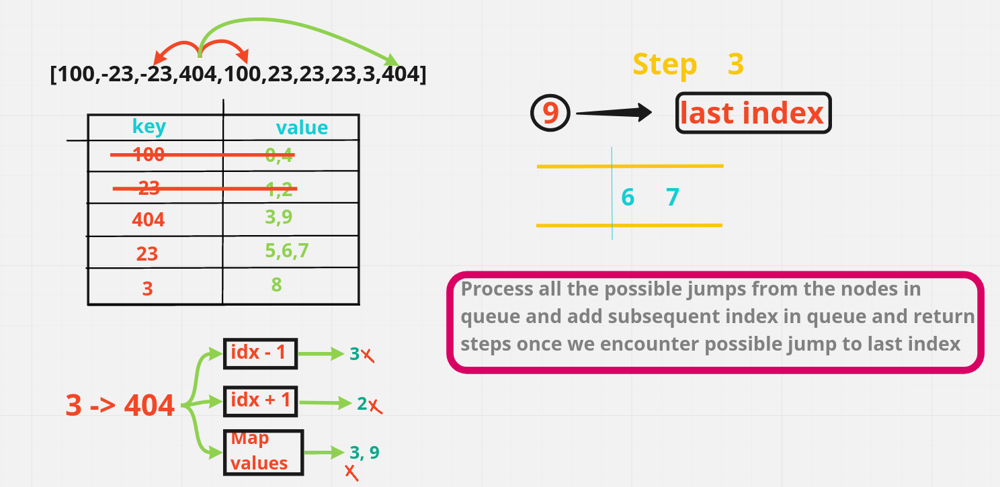
Input:

 arr = [100,-23,-23,404,100,23,23,23,3,404]

Output:

Explanation:

 You need three jumps from index 0 --> 4 --> 3 --> 9. Note that index 9 is the last index of the array.

Approach:

Idea:

The problem Jump Game IV can be treated this problem as a graph problem, where every element i has edges to its adjacent elements i.e., i+1 and i-1, and the index of the elements with the same value. Then we can do a simple BFS starting from the first element until we reach the last index of the array.

We will use a hashmap to store the index of the elements having the same value. Also, we need to keep a visited array to prevent visiting an already visited element. For every iteration, we will be incrementing the answer value as it corresponds to one move. As soon as we encounter the n-1 cell we will return the answer. In the code, we have returned ans-1, as one extra move will be there because we are not checking for the n-1 element while inserting it into the queue.

Code:

Jump Game IV C++ Solution:

class Solution {
public:
    int minJumps(vector<int>& arr) {
        unordered_map<int,vector<int>> mp;
        int n = arr.size();
        for(int i=0;i<n;i++){
            mp[arr[i]].push_back(i);
        }
        
        unordered_set<int> vis;
        queue<int> q;
        q.push(0);
        int ans=0;
        while(!q.empty()){
            ans++;
            int x = q.size();
            for(int i=0;i<x;i++){
                int top = q.front();
                if(top==n-1)
                    return ans-1;
                q.pop();
                if(top<0 or top>=n or vis.count(top)){
                    continue;
                }
                for(auto it:mp[arr[top]]){
                    if(it!=top and !vis.count(it))
                        q.push(it);
                }
                
                q.push(top+1);
                q.push(top-1);
                vis.insert(top);
                mp.erase(arr[top]);
            }
        }
        return ans-1;
    }
};

Jump Game IV Java Solution:

class Solution {
    public int minJumps(int[] arr) {
        int n = arr.length;
        HashMap<Integer, List<Integer>> indicesOfValue = new HashMap<>();
        for (int i = 0; i < n; i++)
            indicesOfValue.computeIfAbsent(arr[i], x -> new LinkedList<>()).add(i);
        boolean[] visited = new boolean[n]; visited[0] = true;
        Queue<Integer> q = new LinkedList<>(); q.offer(0);
        int step = 0;
        while (!q.isEmpty()) {
            for (int size = q.size(); size > 0; --size) {
                int i = q.poll();
                if (i == n - 1) return step; // Reached to last index
                List<Integer> next = indicesOfValue.get(arr[i]);
                next.add(i - 1); next.add(i + 1);
                for (int j : next) {
                    if (j >= 0 && j < n && !visited[j]) {
                        visited[j] = true;
                        q.offer(j);
                    }
                }
                next.clear(); // avoid later lookup indicesOfValue arr[i]
            }
            step++;
        }
        return 0;
    }
}

Complexity Analysis of Jump Game IV Leetcode Solution:

Time Complexity: The time complexity of the above code is $O (n)$ since we will visit every node at most once, where n = size of the input array.
Space Complexity: The space complexity of the above code is $O (n)$ for the vis set and hashmap. A good hashmap allows insertion and deletion in average O(1) time hence an efficient operation.