Longest Common Subsequence LeetCode Solution

Difficulty Level Medium
Frequently asked in Adobe Amazon DoorDash eBay Facebook Google Indeed MicrosoftViews 3840

Problem Statement

Longest Common Subsequence LeetCode Solution – Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.

A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.

  • For example, "ace" is a subsequence of "abcde".

A common subsequence of two strings is a subsequence that is common to both strings.

 

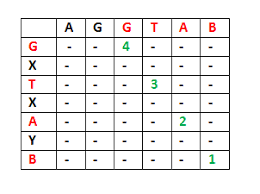
Longest Common Subsequence LeetCode Solution

Example 1:

Input: text1 = "abcde", text2 = "ace" 
Output: 3  
Explanation: The longest common subsequence is "ace" and its length is 3.


Example 2:

Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.


Example 3:

Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.

Explanation

  • The idea is to use dynamic programming.
  • Create a 2D DP array of n+1*m+1 dimensions
  •  I am using the bottom up dp approach so i have iterated from text1.length()-1 to 0 and text2.length()-1 to 0
  • if the characters match,we do 1+ the diagnal value dp[i+1][j+1]
  • else we find the max between left and bottom value max(dp[i][j+1],dp[i+1][j])
  • return the dp[0][0] as it will have the value for longest common Subsequence

Code

Longest Common Subsequence Leetcode Java Solution:

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int [][]dp = new int[text1.length()+1][text2.length()+1];    
        for(int i= text1.length()-1;i>=0;i--){
            for(int j = text2.length()-1;j>=0;j--){
                char ch1 = text1.charAt(i);
                char ch2 = text2.charAt(j);
                if(ch1==ch2) // diagnal
                dp[i][j]= 1+dp[i+1][j+1];
                else// left,down
                    dp[i][j] = Math.max(dp[i][j+1],dp[i+1][j]);
                    
            }
        }
        return dp[0][0];
    }
}

C++ Solution:

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        
//         // base case
//         if( text1.length() == 0 || text2.length() == 0) return 0;
        
//         // recursive call
//         if( text1[0] == text2[0]) return 1 + longestCommonSubsequence( text1.substr(1) , text2.substr(1) );
        
//         else return max(  longestCommonSubsequence( text1.substr(1) , text2  ) ,  longestCommonSubsequence( text1  , text2.substr(1) ));
        
        
        int n = text1.length();
        int m = text2.length();
        
        int dp[n+1][m+1];
        
        for( int i = 0 ; i <= m ; i++) dp[0][i] = 0;
        for( int i = 0 ; i <= n ; i++) dp[i][0] = 0;
        
        for(int i = 1 ; i <= n ; i++){
            
            for( int j = 1 ; j <= m ; j++){
                
                if( text1[i-1] == text2[j-1]) dp[i][j] = 1 + dp[i-1][j-1];
                
                else dp[i][j] = max( dp[i][j-1] , dp[i-1][j]) ;
            }
        }
        
        return dp[n][m];
        
        
    }
};

Complexity Analysis:

  • Time Complexity: o(nm) 
  • Space Complexity :o(nm)

Translate »