Table of Contents
Problem Statement
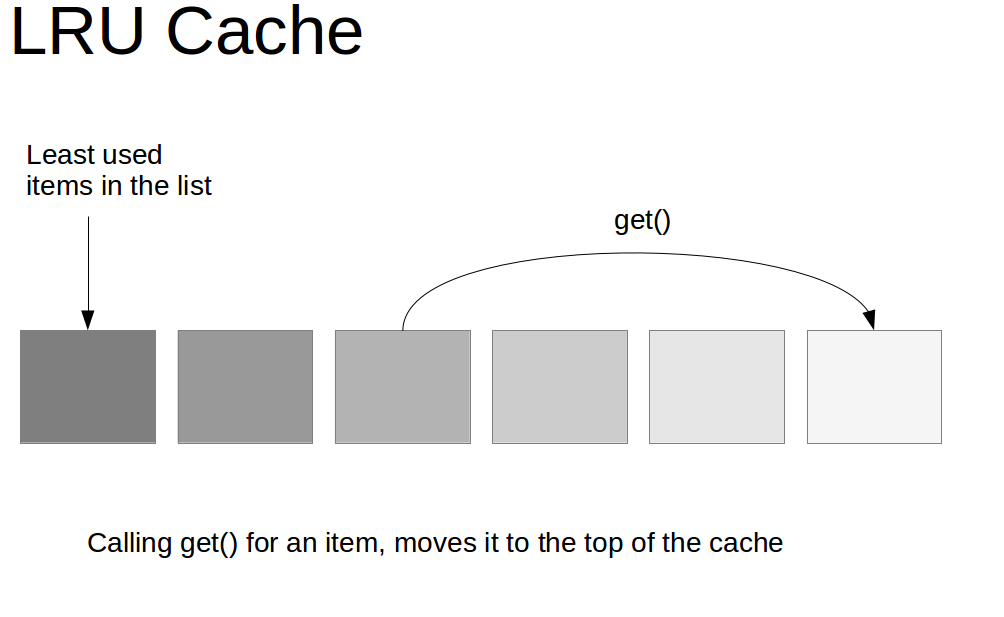
The LRU Cache LeetCode Solution – “LRU Cache” asks you to design a data structure that follows Least Recently Used (LRU) Cache
We need to implement LRUCache class that has the following functions:
- LRUCache(int capacity): Initializes the LRU cache with positive size capacity.
- int get(int key): Return the value of the key if it exists, otherwise return -1.
- void put(int key, int value): update the value of the key if it exists, otherwise insert the key-value pair into the cache. If the size of the cache exceeds the capacity of the cache, then remove the least recently used key.
Example:
Input: ["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]Output: [null, null, null, 1, null, -1, null, -1, 3, 4]
Explanation:
- LRUCache lRUCache = new LRUCache(2);
- lRUCache.put(1,1); [cache is {1=1} ]
- lRUCache.put(2,2); [cache is {1=1,2=2} ]
- lRUCache.get(1); [return 1 ]
- lRUCache.put(3,3); [LRU key was 2, remove key 2, cache is {1=1,3=3} ]
- lRUCache.get(2); [return -1 ]
- lRUCache.put(4,4); [LRU key was 1, remove key 1, cache is {4=4,3=3} ]
- lRUCache.get(1); [return -1 ]
- lRUCache.get(3); [return 3 ]
- lRUCache.get(4); [return 4 ]
Approach
Idea:
- The main idea to solve this problem is to use Hashmap and a doubly linked list.
- Maintain a doubly linked list and a hashmap that keeps a mapping of the key to the node’s address that is present in the double linked list.
- When the constructor is called, initialize the current size of the cache as zero, and create the dummy node of the double linked list. Also, clear the entries of the hashtable.
- updateCache() function is used to update the cache if a certain key is already present in the double linked list and also update the double linked list.
- We will return -1 when get() function is called and the key is not present in the cache, otherwise return the value and update the cache.
- When the put() method is called, and the key is already present in the cache, update the key-value pair and also update the cache and modify the double linked list.
- When the put() method is called and the key is not present in the cache, we’ll create a new node and insert the node in the double linked list and also insert the key-node address in the hash. Also, if the size of the cache exceeds its maximum capacity, we need to remove the least recently used key value from the cache. This can be efficiently done with the help of linked list.
Code
LRU Cache Leetcode C++ Solution:
class LRUCache {
public:
struct Node{
Node* prev;
Node* next;
int data,key;
Node(int key,int data){
this->key = key;
this->data = data;
prev = next = nullptr;
}
};
Node *dummy,*curr;
unordered_map<int,Node*> hash;
int max_size,curr_size;
void updateCache(int key){
if(hash[key]==curr){
return;
}
Node *node1 = hash[key]->prev,*node2 = hash[key]->next;
node1->next = node2;
node2->prev = node1;
curr->next = hash[key];
hash[key]->prev = curr;
hash[key]->next = nullptr;
curr = curr->next;
}
LRUCache(int capacity) {
curr_size = 0;
max_size = capacity;
dummy = new Node(-1,-1);
curr = dummy;
hash.clear();
}
int get(int key) {
if(!hash.count(key)){
return -1;
}
updateCache(key);
return hash[key]->data;
}
void put(int key, int data) {
if(hash.count(key)){
hash[key]->data = data;
updateCache(key);
}
else{
if(curr_size==max_size){
hash.erase(dummy->next->key);
Node *node1 = dummy,*node2 = dummy->next->next;
node1->next = node2;
if(node2!=nullptr){
node2->prev = node1;
}
else{
curr = node1;
}
curr_size--;
}
Node* newNode = new Node(key,data);
curr->next = newNode;
newNode->prev = curr;
curr = curr->next;
hash[key] = newNode;
curr_size++;
}
}
};LRU Cache Leetcode Java Solution:
import java.util.Hashtable;
public class LRUCache {
class DLinkedNode {
int key;
int value;
DLinkedNode pre;
DLinkedNode post;
}
private void addNode(DLinkedNode node) {
node.pre = head;
node.post = head.post;
head.post.pre = node;
head.post = node;
}
private void removeNode(DLinkedNode node){
DLinkedNode pre = node.pre;
DLinkedNode post = node.post;
pre.post = post;
post.pre = pre;
}
private void moveToHead(DLinkedNode node){
this.removeNode(node);
this.addNode(node);
}
private DLinkedNode popTail(){
DLinkedNode res = tail.pre;
this.removeNode(res);
return res;
}
private Hashtable<Integer, DLinkedNode>
cache = new Hashtable<Integer, DLinkedNode>();
private int count;
private int capacity;
private DLinkedNode head, tail;
public LRUCache(int capacity) {
this.count = 0;
this.capacity = capacity;
head = new DLinkedNode();
head.pre = null;
tail = new DLinkedNode();
tail.post = null;
head.post = tail;
tail.pre = head;
}
public int get(int key) {
DLinkedNode node = cache.get(key);
if(node == null){
return -1;
}
this.moveToHead(node);
return node.value;
}
public void put(int key, int value) {
DLinkedNode node = cache.get(key);
if(node == null){
DLinkedNode newNode = new DLinkedNode();
newNode.key = key;
newNode.value = value;
this.cache.put(key, newNode);
this.addNode(newNode);
++count;
if(count > capacity){
DLinkedNode tail = this.popTail();
this.cache.remove(tail.key);
--count;
}
}else{
node.value = value;
this.moveToHead(node);
}
}
}Complexity Analysis for LRU Cache Leetcode Solution
Time Complexity
The time complexity of the above code is O(1) if we use an efficient hash function that allows insertion and deleting in O(1) time. Also, adding and removing nodes from a double-linked list takes O(1) time.
Space Complexity
The space complexity of the above code is O(N) since the maximum size of the hashmap can be O(N).
Reference: https://en.wikipedia.org/wiki/Cache_replacement_policies