Matrix Diagonal Sum Leetcode Solution

Problem Statement

In Matrix Diagonal Sum problem a square matrix of integers is given. We have to calculate the sum of all the elements present at its diagonals i.e. elements at primary diagonal as well as secondary diagonal. Each element should be counted only once.

Example

mat = [[1,2,3],
       [4,5,6],
       [7,8,9]]

25

Explanation:

Diagonals sum: 1 + 5 + 9 + 3 + 7 = 25
Notice that element mat[1][1] = 5 is counted only once

mat = [[1,1,1,1],
       [1,1,1,1],
       [1,1,1,1],
       [1,1,1,1]]

8

Explanation:

Diagonals sum: (1+1+1+1)+(1+1+1+1)=8.

Approach

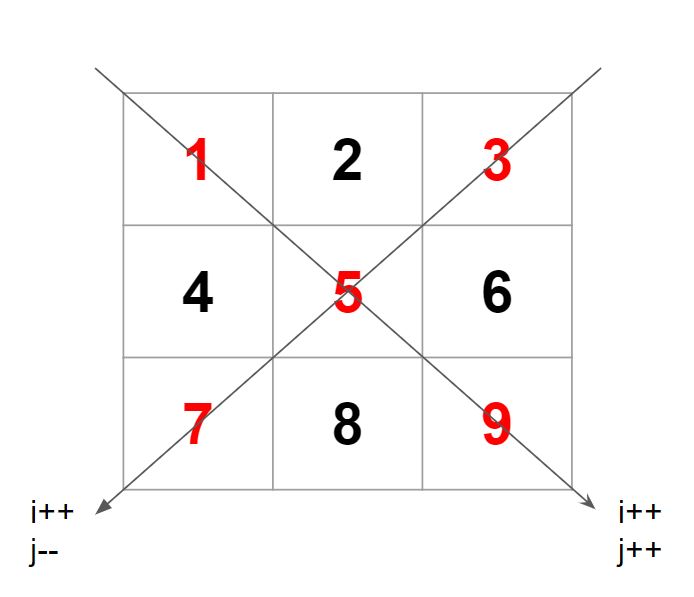
In given square matrix we have to just add the diagonal elements and return its sum.
Lets see what will be the indices pattern in the matrix for diagonal elements. First if we see on the primary diagonal, its first element is on index i=0,j=0 and next element is on (i+1,j+1). Similarly last element will be on index (n-1,n-1) where n is the width of the given square matrix. All indices on this diagonal have i=j.
So we can iterate over this diagonal in a loop as follows:

1. Initialise i=0 and j=0.
2. Run a loop while i<n and j<n.
3. Add the current element. Increment i and j both by 1.

Now lets see for secondary diagonal. index of first element in first row is i=0, j=n-1. Next element is at (i+1.j-1). Similarly last element is at (n-1,0).
So we can iterate over this diagonal in loop as follows:

1. Initialise i=0 and j=n-1.
2. Run a loop while i<n and j>=0.
3. Add the current element ( if it does not lie on primary diagonal, ie. i==j ). Increment i by 1 and decrement j by 1.

Finally return the sum after both the operation.

Implementation

C++ Program for Matrix Diagonal Sum Leetcode Solution

#include <bits/stdc++.h>
using namespace std;

int diagonalSum(vector<vector<int>>& mat) 
{
    int n=mat.size();

    int sum=0;
    int i=0,j=0;

    while(i<n)
    {
        sum+=mat[i][j];
        i++;
        j++;
    }

    i=0;
    j=n-1;

    while(i<n)
    {
        if(i!=j)   sum+=mat[i][j];
        i++;
        j--;
    }

    return sum;
}

int main() 
{
    vector<vector<int>> mat={
            {1,2,3},
            {4,5,6},
            {7,8,9}  
    };
   
    cout<<diagonalSum(mat)<<endl;

  return 0; 
}

25

Java Program for Matrix Diagonal Sum Leetcode Solution

import java.lang.*;

class Rextester
{  
    public static int diagonalSum(int[][] mat) 
    {
        int n=mat.length;
        
        int sum=0;
        int i=0,j=0;
        
        while(i<n)
        {
            sum+=mat[i][j];
            i++;
            j++;
        }
        
        i=0;
        j=n-1;
        
        while(i<n)
        {
          if(i!=j)   sum+=mat[i][j];
            
            i++;
            j--;
        }
        
        return sum;
        
    }
    
    public static void main(String args[])
    {
       int[][] mat={
            {1,2,3},
            {4,5,6},
            {7,8,9}  
        };
    
       System.out.println(diagonalSum(mat));
   
    }
}

25

Complexity Analysis for Matrix Diagonal Sum Leetcode Solution

Time Complexity

O(N) : Here N is the size of the square matrix having N^2 elements. As we are only traversing on both diagonal elements, time complexity will be equal to number of elements present at diagonals ( 2*N ), i.e. O(N).

Space Complexity 

O(1) : Here space complexity is constant as we are not using any extra memory.