Table of Contents
Problem Statement
In this problem, we are given a number made up of digits 6 or 9. We can replace one of a digit of this number and change this to another digit. i.e. we can replace a 6 to 9 or we can replace a 9 to 6. We have to output the maximum number we can get by at most one replace.
Example
num = 9669
9969
Explanation:
Changing the first digit results in 6669.
Changing the second digit results in 9969.
Similarly Changing the third digit results in 9699.
Changing the fourth digit results in 9666.
The maximum number is 9969.
9996
9999
Explanation:
Changing the last digit 6 to 9 results in the maximum number.
Approach
As we can replace a digit to make the number maximum, one thing we can understand here is that, we should replace 6 to 9 only, because 9 to 6 replace will make the number smaller.
Another thing we can understand here is, we should replace a digit leftmost as possible. Let’s understand this thing with an example.
Suppose we have a number given, 6666
We have to replace a digit from 6 to 9 such that the formed number is maximum. If we replace the rightmost 6 then we get 6669.
If we replace the leftmost 6 then we get 9666 which is of course the maximum of all numbers gained by such replacement on this number.
Thus we will try to replace the leftmost 6. And if no 6 is present in given number e.g. 9999 then we will not perform any replace operation.
We can break the given number in form of an array and then we can replace the leftmost 6 by 9 easily. Then we will recreate our new number from the array and output the number.
There is a constraint that the number is limited to 4 digits. Thus we will create an array of size 4 which will satisfy all numbers of smaller length too.
So, the algorithm basically comprises of three main parts.
i) converting number to array: we are doing this by using a while loop with the condition of number>0. Every time, the digit at unit place is stored at the current index of an array and the number is divided by 10.
ii) changing the leftmost 6 to 9 in the array.
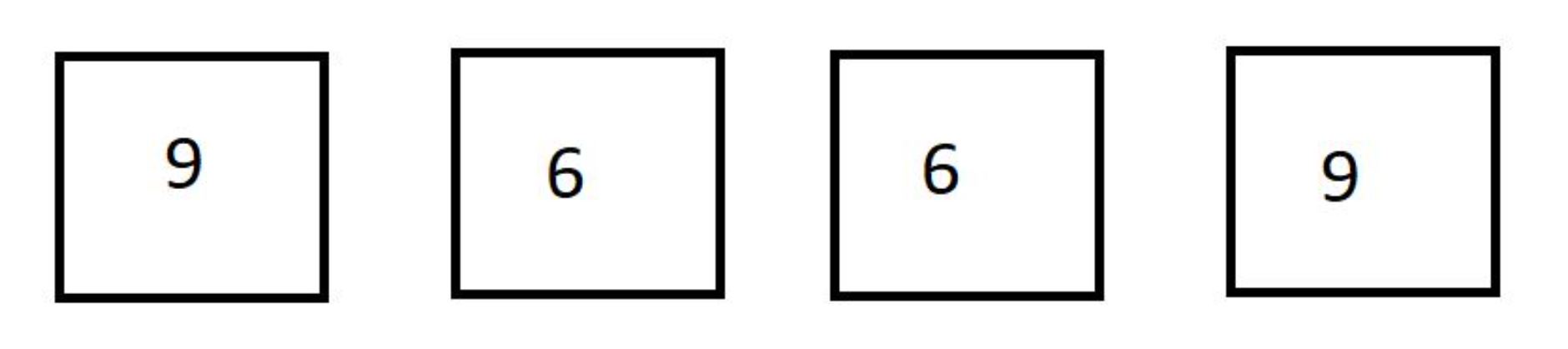
after converting leftmost 6 to 9 :
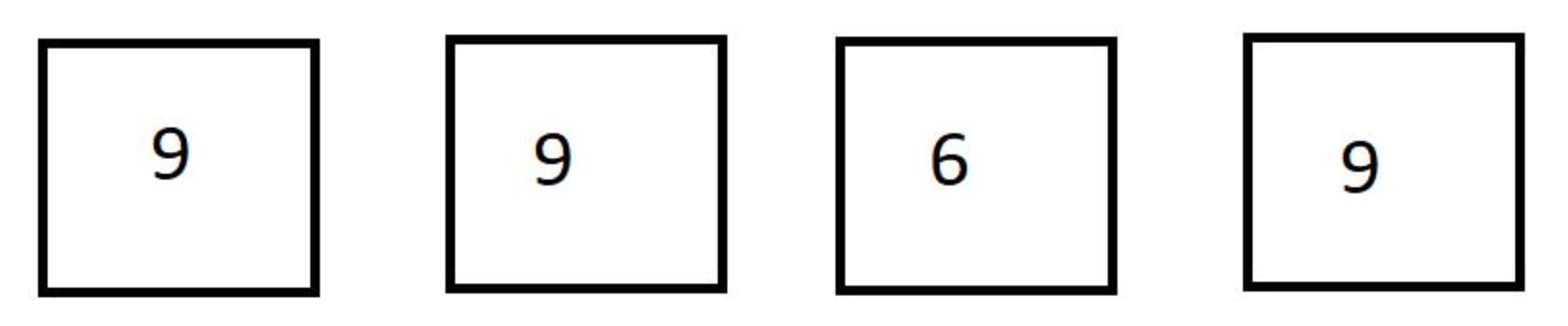
iii) converting array to number: we are doing this by using a loop.
Implementation
C++ Program for Maximum 69 Number Leetcode Solution
#include <iostream>
using namespace std;
int maximum69Number (int num)
{
int arr[4];
fill(arr,arr+4,0);
int i=3;
while(num!=0){
arr[i--]=num%10;
num/=10;
}
for(i=0;i<=3;i++){
if(arr[i]==6){arr[i]=9;break;}
}
int ans=0,mul=1;
for(i=3;i>=0;i--){
ans+=(mul*arr[i]);
mul*=10;
}
return ans;
}
int main()
{
cout << maximum69Number(9669);
}9969
Java Program for Maximum 69 Number Leetcode Solution
import java.util.*;
import java.lang.*;
class Solution
{
public static int maximum69Number (int num)
{
int[] arr=new int[4];
int i=3;
while(num!=0){
arr[i--]=num%10;
num/=10;
}
for(i=0;i<=3;i++){
if(arr[i]==6){arr[i]=9;break;}
}
int ans=0,mul=1;
for(i=3;i>=0;i--){
ans+=(mul*arr[i]);
mul*=10;
}
return ans;
}
public static void main(String args[])
{
System.out.println(maximum69Number(9669));
}
}9969
Complexity Analysis for Maximum 69 Number Leetcode Solution
Time Complexity
O(1): We are performing 3 loops of 4 iterations at max. Thus, this is also constant time for this question. However, if the constraint would be high, we would use an array of size equal to the length of the number. At that time our time complexity would be O(length of number).
Space Complexity
O(1): We have used an extra array of size 4 which is constant. Thus space complexity is O(1).