Maximum Depth of Binary Tree Leetcode Solution.

Table of Contents

Problem Statement

In the problem a binary tree is given and we have to find out the maximum depth of the given tree. A binary tree’s maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

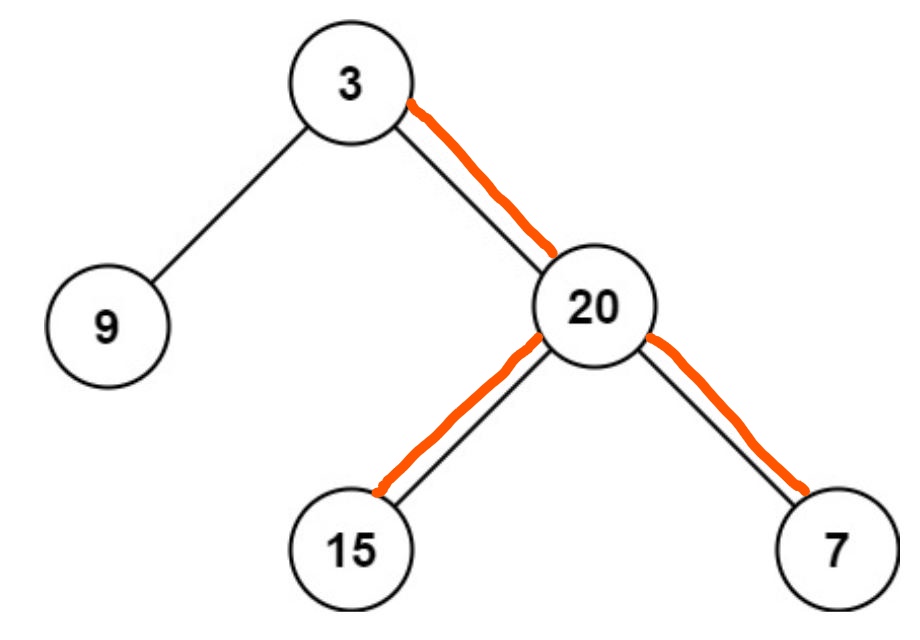
Example

Explanation: There are two possible longest path as shown in below tree in red color.

Empty Tree

As the tree is empty, depth is 0.

As there are only one node, depth is 1.

Approach

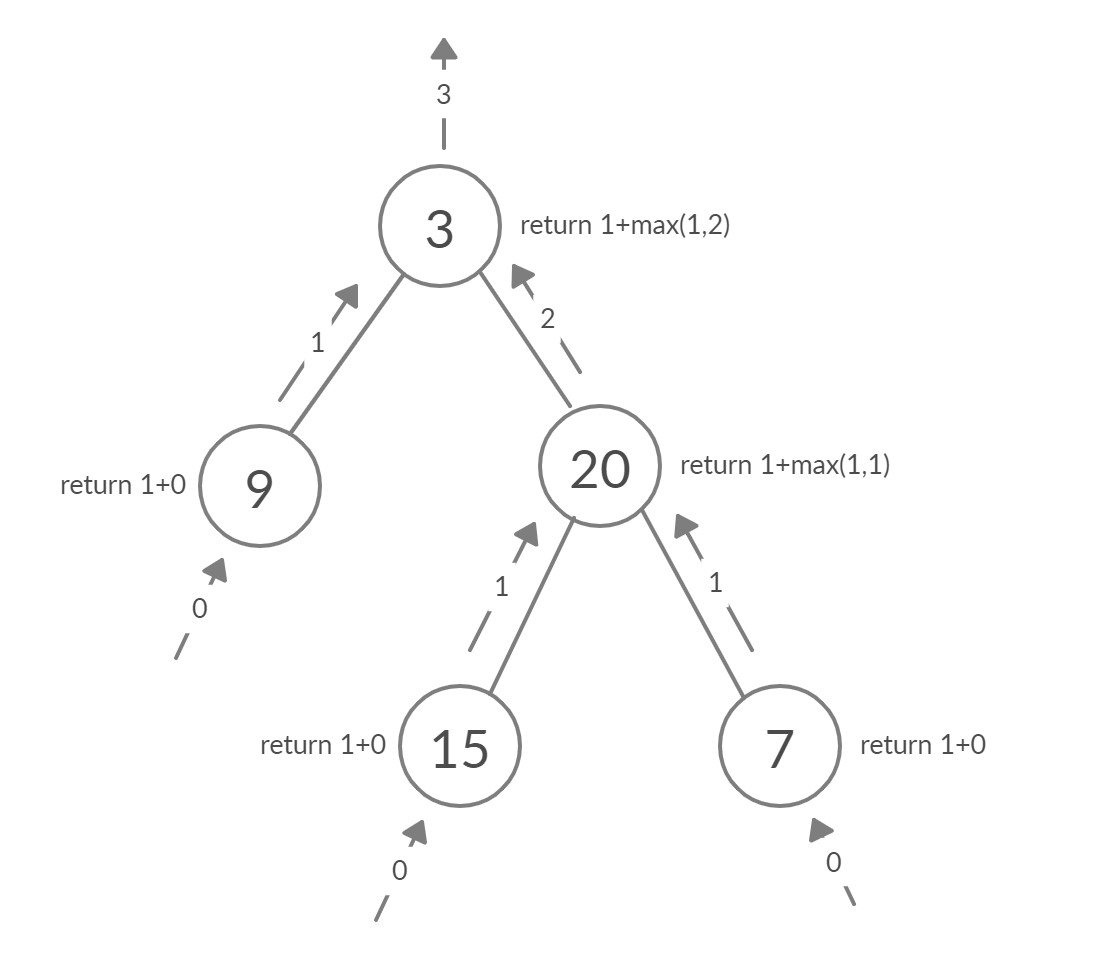
To find the maximum depth of the tree we can apply a simple recursive approach. Where each function call will represent a subtree which has root node called as ‘root’. We traverse the tree by a recursive function starting from the root node.

So the base case is when the subtree is empty i.e. root is NULL. So we return depth as 0.

if root is not NULL, call the same function recursively for its left child and right child.

As shown in figure, when the two child function return its depth we pick the maximum out of these two subtrees and return this value after adding 1 to it ( Adding current node which is the parent of the two subtrees).

Implementation

C++ Program for Maximum Depth of Binary Tree Leetcode Solution

#include <bits/stdc++.h>
using namespace std;
struct TreeNode {
  int val;
  TreeNode *left;
  TreeNode *right;
  TreeNode() : val(0), left(nullptr), right(nullptr) {}
  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

int maxDepth(TreeNode* root) 
{
    if(root==NULL) return 0;
    return 1+max(maxDepth(root->left),maxDepth(root->right));
}

int main() 
{
    TreeNode *root= new TreeNode(3);
    root->left= new TreeNode(9);
    root->right= new TreeNode(20);
    root->right->left= new TreeNode(15);
    root->right->right= new TreeNode(7);
    
    cout<<maxDepth(root)<<endl; 
  return 0; 
}

Java Program for Maximum Depth of Binary Tree Leetcode Solution

import java.util.*;
import java.lang.*;
class TreeNode 
{
      int val;
      TreeNode left;
      TreeNode right;
      TreeNode() {}
      TreeNode(int val) { this.val = val; }
      TreeNode(int val, TreeNode left, TreeNode right) 
      {
          this.val = val;
          this.left = left;
          this.right = right;
      }
}

class MaxDepth
{  
    public static int maxDepth(TreeNode root) 
    {
        if(root==null) return 0;
        
        return 1+Math.max(maxDepth(root.left),maxDepth(root.right));
    }
    
    public static void main(String args[])
    {
        TreeNode root= new TreeNode(3);
        root.left= new TreeNode(9);
        root.right= new TreeNode(20);
        root.right.left= new TreeNode(15);
        root.right.right= new TreeNode(7);
       
        System.out.println(maxDepth(root));
        
    }
}

Complexity Analysis for Maximum Depth of Binary Tree Leetcode Solution

Time Complexity

O(N) : we visit each node exactly once, thus the time complexity is O(N), where N is the total number of nodes in the given tree.

Space Complexity

O(N) : In the worst case, the tree is completely unbalanced, e.g. each node has only left child node or only right child node, then recursion call would occur N times (the height of the tree). Therefore the maximum size of call stack would be O(N).
In the best case (the tree is completely balanced), the height of the tree would be log⁡(N). Therefore, the space complexity in this case would be O(log⁡(N).