Maximum Product of Two Elements in an Array Leetcode Solution

Difficulty Level Easy
Frequently asked in Samsung
algorithms Array coding Interview interviewprep LeetCode LeetCodeSolutionsViews 4381

In the problem “Maximum Product of Two Elements in an Array”, our goal is to find two indices i and j in a given array of integers a, such that the product (a[i] – 1) * (a[j] – 1) is maximum. The array has at least 2 elements and all elements are positive. The problem that the required product fits in the integer range. We need to print the value of (a[i] – 1) * (a[j] – 1) for optimal i & j.

Example

a = {1 , 4 , 5 , 3 , 6 , 4}

2

Explanation

Clearly, 6 and 5 are the largest and the second-largest numbers. So, product = (a[i] – 1) * (a[j] – 1) = 20.

Approach(Sorting)

The product: (a[i] – 1) * (a[j] – 1) will be maximum when a[i] and a[j] are the two largest elements in the array. Instead of finding two indices i and j containing the two greatest elements, we can sort the array in ascending order. This will make sure that the two largest elements are at the end. Hence, the product (a[n – 1] – 1) * (a[n – 2] – 1) will be the required result.

Algorithm

  1. Sort the array
  2. Print the result: (a[n – 1] – 1) * (a[n – 2] – 1)

Implementation of algorithm to find Maximum Product of Two Elements in an Array

C++ Program

#include <bits/stdc++.h>
using namespace std;

int maxProduct(vector <int> &a)
{
    int n = a.size();
    sort(a.begin() , a.end());
    return ((a[n - 1] - 1) * (a[n - 2] - 1));
}


int main()
{
    vector <int> a = {1 , 4 , 5 , 3 , 6 , 4};
    cout << maxProduct(a) << '\n';
}

Java Program

import java.util.Arrays;

class maximum_product
{
    public static void main(String args[])
    {
        int[] a = {1 , 4 , 5 , 3 , 6 , 4};
        System.out.println(maxProduct(a));
    }

    static int maxProduct(int[] a)
    {
        int n = a.length;
        Arrays.sort(a);
        return (a[n - 1] - 1) * (a[n - 2] - 1);
    }
}

20

Complexity Analysis of finding Maximum Product of Two Elements in an Array

Time Complexity

O(NlogN), N = size of the array. We sort the array which takes O(NlogN) time.

Space complexity

O(1), as we use constant memory space.

Approach(Optimal)

As we discussed above, we need to find the two greatest elements in the array. By sorting the whole array, we overdo the required work. So, it is optimal to find the first and second-largest element in the array by simple comparing operations. Hence, the required result can be obtained as (firstMax – 1) * (secondMax – 1).

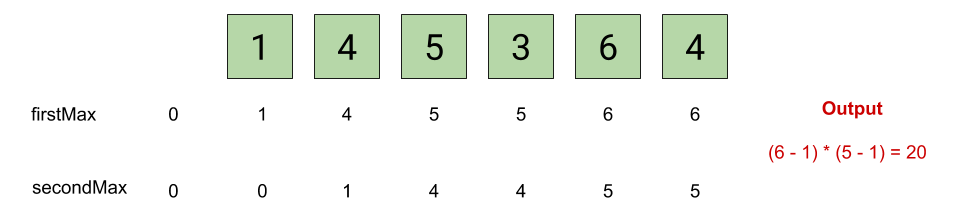
Maximum Product of Two Elements in an Array Leetcode Solution

Algorithm

  1. Initialize two variables: firstMax and secondMax as zero(so that any value in the array updates them intially).
  2. Run a loop from the start of the array to its end.
  3. For every element:
    • Check if it is greater than firstMax:
      • If true:
        • Set secondMax = firstMax
        • Update firstMax = current-element
      • Else:
        • If it is greater than secondMax
          • Update secondMax = current-element
  4. Print the result

Implementation of algorithm to find Maximum Product of Two Elements in an Array Leetcode Solution

C++ Program

#include <bits/stdc++.h>
using namespace std;

int maxProduct(vector <int> &a)
{
    int firstMax = 0 , secondMax = 0 , n = a.size();
    for(int i = 0 ; i < n ; i++)
        if(a[i] > firstMax)
        {
            secondMax = firstMax;
            firstMax = a[i];
        }
        else if(a[i] > secondMax)
            secondMax = a[i];

    return (firstMax - 1) * (secondMax - 1);
}

int main()
{
    vector <int> a = {1 , 4 , 5 , 3 , 6 , 4};
    cout << maxProduct(a) << '\n';
}

Java Program

class maximum_product
{
    public static void main(String args[])
    {
        int[] a = {1 , 4 , 5 , 3 , 6 , 4};
        System.out.println(maxProduct(a));
    }

    static int maxProduct(int[] a)
    {
        int firstMax = 0 , secondMax = 0 , n = a.length;
        for(int i = 0 ; i < n ; i++)
            if(a[i] > firstMax)
            {
                secondMax = firstMax;
                firstMax = a[i];
            }
            else if(a[i] > secondMax)
                secondMax = a[i];

        return (firstMax - 1) * (secondMax - 1);
    }
}

20

Complexity Analysis of finding Maximum Product of Two Elements in an Array Leetcode Solution

Time Complexity

O(N), N = Size of the array. We run a linear loop for simple compare operations.

Space complexity

O(1), as constant memory is used.

Translate »