Maximum Profit in Job Scheduling Leetcode Solution

Difficulty Level Hard
Frequently asked in Airbnb Amazon Atlassian DoorDash Google Microsoft Swiggy Uber
Array Binary Search Dynamic Programming SortingViews 8621

Problem Statement

The Maximum Profit in Job Scheduling LeetCode Solution – “Maximum Profit in Job Scheduling” states that you’re given n jobs where each job starts from startTime[i] and ends at endTime[i] and obtaining the profit of profit[i].

We need to return the maximum profit that we can have such that no two chosen jobs overlap. Also, if a job ends at a time x, then we can start another job at a time greater than or equal to x.

Example:

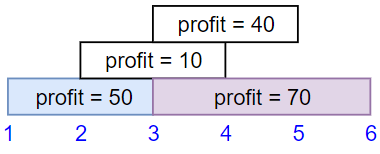
Maximum Profit in Job Scheduling Leetcode Solution

Input:  startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120

Explanation:

  • If we choose the first and fourth jobs, we can get a profit of 120 and, this is the maximum profit we can get.
  • Note that the first and fourth jobs can be done simultaneously since they don’t overlap.
Input:  startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150

Explanation:

  • If we choose the first, fourth and fifth job, we’ll get the maximum profit of 150.
  • Note that the subset chosen doesn’t overlap.

Approach

Idea:

  1. The main idea to solve this problem is to use dynamic programming and binary search.
  2. First of all, we need to sort the jobs in non-decreasing order of their ending time which will help in calculating the maximum profit easily through dynamic programming.
  3. Let dp[i] = maximum profit we can have if we consider first i+1 jobs.
  4. There are two cases for each index:
    1. Choose the current job: If we choose the current job then, this job will start from its startTime[i]. So, the maximum profit we can have is the current profit + dp[j]. dp[j] is the largest index j such that endTime[j] is less than or equal to startTime[i] and j must be strictly less than i. Note that if a valid j exists, then dp[i] = current profit + dp[j] otherwise, dp[i] = current profit.
      1. To calculate the largest index j such that endTime[i] is less than or equal to startTime[i] and j<i, perform the binary search to find the suitable index since the jobs are already sorted in non-decreasing order of their end time.
    2. Don’t Choose the current job: In this case, dp[i] = dp[i-1].
  5. We need to take the maximum of both the above cases for calculating the values for each index.
  6. Our answer will be dp[n-1].

Code

Maximum Profit in Job Scheduling Leetcode C++ Solution:

class Solution {
public:
    int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {
        int n = startTime.size();
        vector<vector<int>> jobs;
        for(int i=0;i<n;i++){
            jobs.push_back({startTime[i],endTime[i],profit[i]});
        }
        sort(jobs.begin(),jobs.end(),[&](const vector<int>& a,const vector<int>& b){
           if(a[1]==b[1]){
               return a[0] < b[0];
           } 
           return a[1] < b[1];
        });
        vector<int> dp(n);
        dp[0] = jobs[0][2];
        for(int i=1;i<n;i++){
            dp[i] = dp[i-1];
            int l = 0,r = i - 1,prev = 0;
            while(l<=r){
                int mid = (l+r)/2;
                if(jobs[mid][1]<=jobs[i][0]){
                    prev = dp[mid];
                    l = mid + 1;
                }
                else{
                    r = mid - 1;
                }
            }
            dp[i] = max(dp[i],jobs[i][2]+prev);
        }
        return dp[n-1];
    }
};

Maximum Profit in Job Scheduling Leetcode Java Solution:

class Solution {
    public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
        int n = startTime.length;
        int[][] jobs = new int[n][3];
        for(int i=0;i<n;i++){
            jobs[i] = new int[] {startTime[i],endTime[i],profit[i]};
        }
        Arrays.sort(jobs,(a,b)->a[1]-b[1]);
        int[] dp = new int[n];
        dp[0] = jobs[0][2];
        for(int i=1;i<n;i++){
            dp[i] = dp[i-1];
            int l = 0,r = i - 1,prev = 0;
            while(l<=r){
                int mid = (l+r)/2;
                if(jobs[mid][1]<=jobs[i][0]){
                    prev = dp[mid];
                    l = mid + 1;
                }
                else{
                    r = mid - 1;
                }
            }
            dp[i] = Math.max(dp[i],jobs[i][2]+prev);
        }
        return dp[n-1];
    }
}

Complexity Analysis for Maximum Profit in Job Scheduling Leetcode Solution

Time Complexity

The time complexity of the above code is O(NlogN) since we traverse the entire input array once and for each index, we’re applying binary search. Here, N = size of the input array.

Space Complexity

The space complexity of the above code is O(N). We’re using a linear array to store the computed values.

Translate »