Maximum Subarray Leetcode Solution

Table of Contents

Problem Statement

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example

nums = [-2,1,-3,4,-1,2,1,-5,4]

Explanation:

[4,-1,2,1] has the largest sum = 6.

nums = [-1]

-1

Approach 1 (Divide and Conquer)

In this approach we will be discussing about divide and conquer technique to solve this problem. We are trying to find that contiguous subarray which has maximum sum. So we can say that the optimum subarray may lie in any part of the array. So we make three cases which will cover all possibilities:

Case 1:
Max subarray lies completely in the left half of the array.
Case 2:
Max subarray lies completely in the right half of the array.
Case 3:
Partial portion of max subarray lies in the left half and another partial portion of it lies in the second half (i.e. subarray is crossing the mid element of the array)

As we can see case 1 and case 2 is basically a subproblem of N/2 sized array having same definition as main problem. Where N is the size of the current array. So we can simply recurs the function over two halves of the array.
Now the main part is case 3 which we have to solve in the current function and then we can return the maximum sum out of these 3 cases.

Lets see how we can solve for case 3:

Suppose we have array = [-2,1,-3,4,-1,2,1,-5,4]
We find mid index to divide it into two equal halves.
mid index = (0+9)/2 = 4

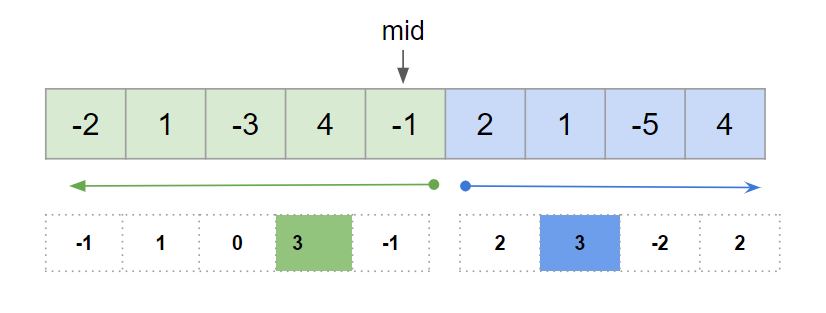
As case 3 is saying that max sum will cross the mid element. So we will try to find the max sum starting at mid and ending at left side. Similarly we will find the max sum starting at (mid+1) and ending at right side. In this way we will find the max subarray which is crossing the mid boundary for case 3.

Algorithm:

Divide the array into two halves.
Recursively find the maximum subarray sum for left subarray.
Recursively find the maximum subarray sum for right subarray.
Find the maximum subarray sum that crosses the midpoint.
Return the maximum of above three sums.

Implementation for Maximum Subarray Leetcode Solution

C++ Program

#include <bits/stdc++.h>
using namespace std;

int helper(int i,int j, vector<int>& nums)
{
    if(i==j) return nums[i];
    int left_cross=INT_MIN, right_cross=INT_MIN;

    int mid= (i+j)/2;
    int cur=0;
    for(int k=mid+1;k<=j;k++)
    {
        cur+= nums[k];
        right_cross= max(right_cross,cur);
    }

    cur=0;
    for(int k=mid;k>=i;k--)
    {
        cur+= nums[k];
        left_cross= max(left_cross,cur);
    }

    int cross_sum = left_cross + right_cross;
    int left_sum  = helper(i,mid,nums);
    int right_sum = helper(mid+1,j,nums);

    return max( cross_sum , max(left_sum , right_sum) );
}

int maxSubArray(vector<int>& nums) {
    return helper(0,nums.size()-1,nums);
}

int main() 
{
    vector<int> nums={-2,1,-3,4,-1,2,1,-5,4};
    cout<< maxSubArray(nums) <<endl;
    return 0; 
}

Java Program

class Rextester{
    
  static int helper(int i,int j, int[] nums)
    { 
        if(i==j) return nums[i];       
        int left_cross=Integer.MIN_VALUE, right_cross=Integer.MIN_VALUE;
        
        int mid= (i+j)/2;
        int cur=0;
        for(int k=mid+1;k<=j;k++)
        {
            cur+= nums[k];
            right_cross= Math.max(right_cross,cur);
        }
        
        cur=0;
        for(int k=mid;k>=i;k--)
        {
            cur+= nums[k];
            left_cross= Math.max(left_cross,cur);
        }
        
        int cross_sum=  left_cross + right_cross; 
        int left_sum = helper(i,mid,nums);
        int right_sum = helper(mid+1,j,nums);
        
        return Math.max( cross_sum , Math.max(left_sum , right_sum) );        
    }
    
    public static int maxSubArray(int[] nums) {
        return helper(0,nums.length-1,nums);
    }
    
  public static void main(String args[])
    {
       	int[] nums={-2,1,-3,4,-1,2,1,-5,4};
    System.out.println(maxSubArray(nums));
    }
}

Complexity Analysis for Maximum Subarray Leetcode Solution

Time Complexity

O(NlogN) : In divide and conquer actually we are dividing the problem into two equal halves of size N/2. Again it is dividing in size of N/4 and so on. Hence the deepest level of recursion will be logN where size of array will be 1 and we are returning from there. At each level we are doing O(n) task hence total time complexity will be O(NlogN). Here the recurrence relation is

Space Complexity

O(logN) : logN space is used for recursion stack.

Approach 2 (Kadane’s method)

Kadane’s method is a famous algorithm for sub array sum. In this method we just iterate once over the given input array. We take a current sum initially with value zero and add each element in the path. We add each element to the current sum if the previous current sum is not negative or otherwise we just break the continuity and update the current sum with current element. Along with it at each position we check if the current sum is also global maximum or not and update the global maximum according to that.

Algorithm:

Create a variable to store global maximum. Initialise with most negative number(INT_MIN).
Create a variable to store current sum. Initialise with zero.
Run a loop from left to right over the array. If current sum has become negative then update it with value 0.
Add the current element to current sum and update the global maximum if current sum is greater than global maximum.
Return the global maximum.

Implementation for Maximum Subarray Leetcode Solution

C++ Program

#include <bits/stdc++.h>
using namespace std;

int maxSubArray(vector<int>& nums) 
{
    int max_sum=INT_MIN;
    int cur=0;
    for(auto x:nums)
    {
        if(cur<0) cur=0;
        cur += x;
        max_sum =  max(max_sum , cur);
    }
    return max_sum;
}

int main() 
{
    vector<int> nums={-2,1,-3,4,-1,2,1,-5,4};
    cout<< maxSubArray(nums) <<endl;
    return 0; 
}

Java Program

class Rextester{
  
    public static int maxSubArray(int[] nums) 
    {
        int max_sum = Integer.MIN_VALUE;
        int cur=0;
        for(int x:nums)
        {
            if(cur<0) cur=0;
            cur += x;
            max_sum =  Math.max(max_sum , cur);
        }
        return max_sum;
    }
    
  public static void main(String args[])
    {
       	int[] nums={-2,1,-3,4,-1,2,1,-5,4};
    System.out.println(maxSubArray(nums));
    }
}