Table of Contents
Problem statement
Median of Two Sorted Arrays LeetCode solution – In the problem “Median of Two Sorted Arrays”, we are given two sorted arrays nums1 and nums2 of size m and n respectively, and we have to return the median of the two sorted arrays.
The overall run time complexity should be O(log (m+n)).
Example
nums1 = [1,3], nums2 = [2]
2.00000
Explanation: Merged array = [1,2,3] and median is 2.
Approach
To solve this problem, we need to first understand what actually does the median do.
It is the partitioning of set into two equal length subsets such that one subset is greater than the other.
i.e., partition the set into two subsets such that every element of one subset is greater than every element of the other subset.
Now come back to the problem, we need to find the median of two sorted arrays.
Can we find a partition for array A and B, such that the length of subsets obtained by adding left of both partitions and right of both partitions are equal?
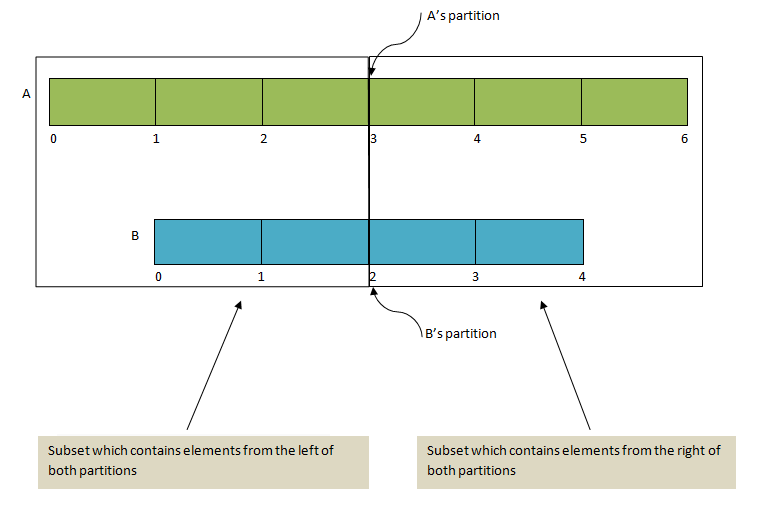
Partitioning an array at the ith position also denotes the number of elements from that array that are present in the left subset.
And as we know that the length of subsets obtained should be equal, hence partitionA + partitionB = (length(A) +length(B)+1)/2
(If the length of the final merged sorted array is odd then, left subset would have more elements)
Now the only thing left is to check how to partition the given two arrays such that the right subset is greater than the left subset.
Let’s define the perfect partition of sorted arrays:
Let say we have array A( length n) and an array B( length m )
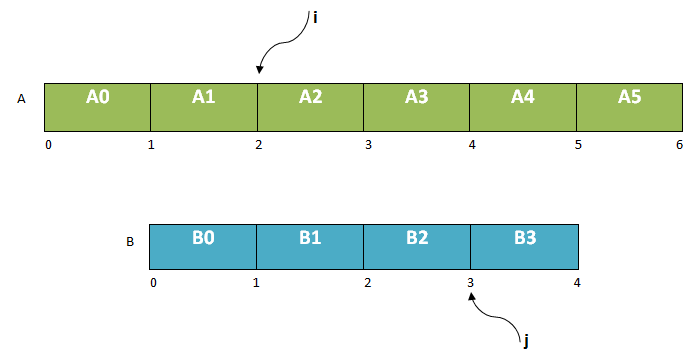
We have partitioned A at i and B at j, then
A perfect partition is when:
- i+j = (n+m+1)/2 (subsets are of equal length)
- A[i-1]<=B[j] (elements of A in the left of i will come in the left subset)
- B[j-1]<=A[i] (elements of B in the left of j will come in left subset)
If A[i-1]>B[j] that means there are some elements in the left of A’s partition that should be placed in the greater(right) subset. In that case, we will move i towards left and j towards the right.
If B[j-1]>A[i] that means there are some elements in the left of B’s partition which should be placed in the greater(right) subset. In that case, we will move j towards the left and i toward the right.
Code
C++ code for Median of two sorted arrays
#include <bits/stdc++.h>
using namespace std;
double findMedianSortedArrays(vector<int>& A, vector<int>& B) {
long n = A.size(), m = B.size(), t=(n+m+1)/2;
if(n>m)return findMedianSortedArrays(B,A);
if(n==0) return m % 2 == 0 ? (double)(B[m/2 - 1] + B[m/2]) / 2 : B[m/2];
if(m==0) return n % 2 == 0 ? (double)(A[n/2 - 1] + A[n/2]) / 2 : A[n/2];
long left = 0, right = n;
while (left <= right) {
long partitionA = left + (right-left)/2;
long partitionB = t - double(partitionA); // partitionA + partitionB = (n+m+1)/2
//if partitionA is 0 then take INT_MIN for maxLeftA (nothing is left in the left of partition)
double maxLeftA = INT_MIN;
if(partitionA > 0){
maxLeftA = A[partitionA-1];
}
//if partitionA is n then take INT_MAX for minRightA (nothing is left in the right of partition)
double minRightA = INT_MAX;
if(partitionA < n){
minRightA = A[partitionA];
}
//Similarly for maxLeftB and minrightB
double maxLeftB = INT_MIN;
if(partitionB > 0){
maxLeftB = B[partitionB-1];
}
double minRightB = INT_MAX;
if(partitionB < m){
minRightB = B[partitionB];
}
if (maxLeftA <= minRightB && maxLeftB <= minRightA) { // check weather it's a perfect partition or not
if ((n+m) % 2 == 0) { // if the sorted merged array is of even length
return (max(maxLeftA, maxLeftB) + min(minRightA, minRightB))/2.0;
}
else {
return max(maxLeftA, maxLeftB);
}
}
else if (maxLeftA > minRightB) { //move left side.
right = partitionA - 1;
}
else { // move right side
left = partitionA + 1;
}
}
return 0.0; // we can't find the median if input is invalid i.e., arrays are not sorted
}
int main() {
vector<int> A = {1, 2, 3, 5, 6};
vector<int> B = {4};
cout<<findMedianSortedArrays(A, B);
return 0;
}3.50000
Java code for Median of two sorted arrays
import java.util.Scanner;
public class Main{
public static double findMedianSortedArrays(int A[], int B[]) {
int n = A.length, m = B.length;
if(n>m)return findMedianSortedArrays(B,A);
int left = 0, right = n;
while (left <= right) {
int partitionA = (left + right)/2;
int partitionB = (n + m + 1)/2 - partitionA; // partitionA + partitionB = (n+m+1)/2
//if partitionA is 0 then take INT_MIN for maxLeftA (nothing is left in the left of partition)
double maxLeftA = Integer.MIN_VALUE;
if(partitionA > 0){
maxLeftA = A[partitionA-1];
}
//if partitionA is n then take INT_MAX for minRightA (nothing is left in the right of partition)
double minRightA = Integer.MAX_VALUE;
if(partitionA < n){
minRightA = A[partitionA];
}
//Similarly for maxLeftB and minrightB
double maxLeftB = Integer.MIN_VALUE;
if(partitionB > 0){
maxLeftB = B[partitionB-1];
}
double minRightB = Integer.MAX_VALUE;
if(partitionB < m){
minRightB = B[partitionB];
}
if (maxLeftA <= minRightB && maxLeftB <= minRightA) { // check weather it's a perfect partition or not
if ((n+m) % 2 == 0) { // if the sorted merged array is of even length
return (Math.max(maxLeftA, maxLeftB) + Math.min(minRightA, minRightB))/2.0;
}
else {
return Math.max(maxLeftA, maxLeftB);
}
}
else if (maxLeftA > minRightB) { //move left side.
right = partitionA - 1;
}
else { // move right side
left = partitionA + 1;
}
}
return 0.0; // we can't find the median if input is invalid i.e., arrays are not sorted
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int A[]=new int[]{1,2,6,8};
int B[]=new int[]{5,7,10};
double median = findMedianSortedArrays(A,B);
System.out.println(median);
}
}6.000
Complexity Analysis for Median of Two Sorted Arrays LeetCode solution
Time Complexity: O(log(n))
as at every step, we are reducing the search space by half (either choosing left search space or right search space from the middle index).
Space Complexity: O(1)
because we just use some variables for calculation.
Thanks for reading the Median of Two Sorted Arrays LeetCode solution!!
Reference – https://en.wikipedia.org/wiki/Array_data_structure