Min Stack Leetcode Solution

Problem Statement

Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.

push(x) — Push element x onto stack.
pop() — Removes the element on top of the stack.
top() — Get the top element.
getMin() — Retrieve the minimum element in the stack.

Note: Methods pop, top and getMin operations will always be called on non-empty stacks.

Example

push(-2);
push(0);
push(-3);
getMin();
pop();
top();
getMin();

-3
0
-2

Explanation:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   // return -3
minStack.pop();
minStack.top();          // return 0
minStack.getMin();   // return -2

Approach

We know a stack is a data structure in which we can easily push an element at the end and also easily access or pop the last inserted element. These operations happens in O(1) time in a stack. But in this problem we have to make an extra function getMin that should be able to retrive the minimum element in the stack and that also in O(1) time.

So to design this data structure we will obviously use stack as main data structure but we have to add some extra algorithm to it so that we are able to get minimum element in constant time.

For this, lets see an example. Let suppose we have to insert these elements in stack in order :
5 6 4 7 5 3 , and then start popping.

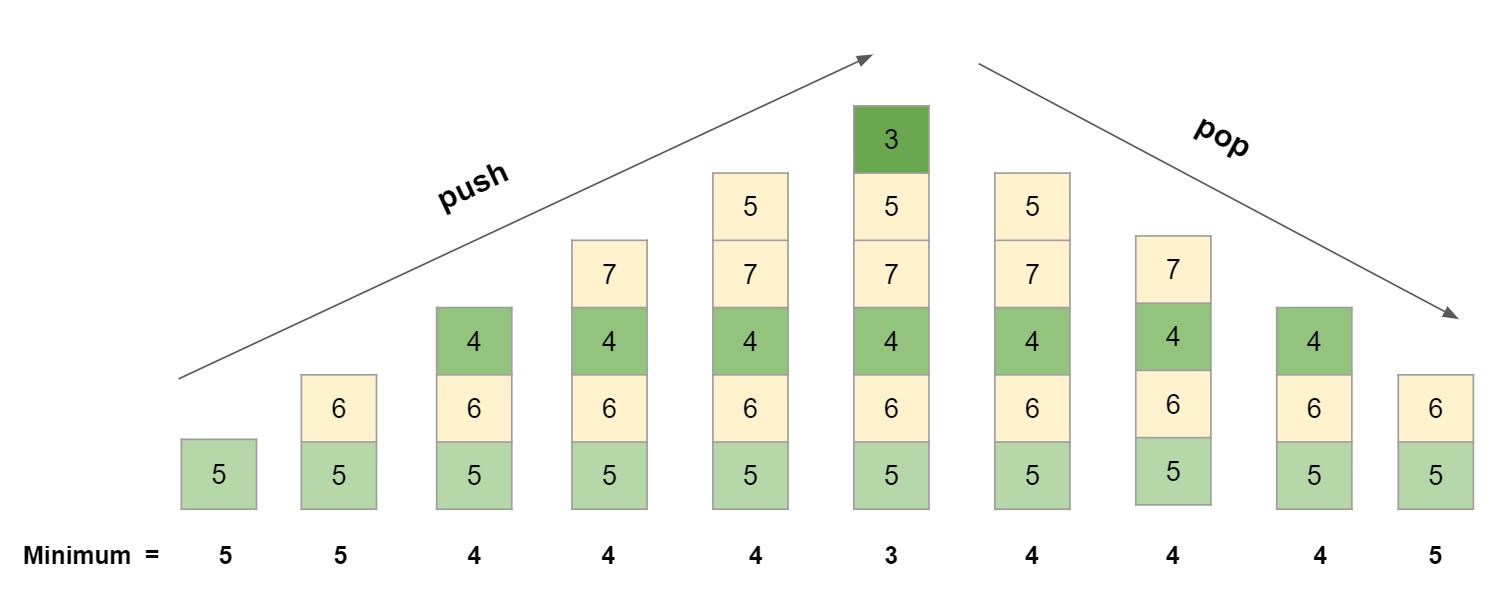
We can observe that when we pop the element which is also current minimum then the new minimum is the same as it was while before pushing it. So we must have the knowledge of all the previous minimum elements till now so that we can retrieve the minimum after removal of current minimum element in O(1) time.

For this we can use another stack which will store only the minimum element(represented with green colour in fig) of the main stack . So the top element of the minimum stack will tell the current minimum element.

During insertion or removal of an element we will update the min stack as below:

• If the new pushed element is less than or equal to current minimum then we push this element into min stack also to update the current minimum.
• If the popped element is equal to the current minimum then then we remove this element from the min stack also to update the current minimum.

Implementation

C++ Program for Min Stack Leetcode Solution

#include <bits/stdc++.h>
using namespace std;

class MinStack {
public:
    stack<int> st,mn;
    
    void push(int x) 
    {
        if(st.empty() || x<=mn.top())
            mn.push(x);
        st.push(x);
    }
    
    void pop() 
    {
        if(st.top()==mn.top()) 
            mn.pop();
        st.pop();
    }
    
    int top() 
    {
        return st.top();
    }
    
    int getMin() 
    {
        return mn.top();
    }
};

int main() 
{
    MinStack* minStack = new MinStack();
    minStack->push(-2);
    minStack->push(0);
    minStack->push(-3);
    int param1 = minStack->getMin(); 
    minStack->pop();
    int param2 = minStack->top();   
    int param3 = minStack->getMin(); 
    
    cout<<param1<<endl;
    cout<<param2<<endl;
    cout<<param3<<endl;
    
    return 0; 
}

-3
0
-2

Java Program for Min Stack Leetcode Solution

import java.util.*;
class MinStack {

    Stack<Integer> st=new Stack<>();
    Stack<Integer> mn=new Stack<>();
   
    public void push(int x) 
    {
        if(st.empty() || x<=mn.peek())
            mn.push(x);
        st.push(x);
    }
    
    public void pop() 
    {
        if(st.peek().equals(mn.peek())) 
            mn.pop();
        st.pop();
    }
    
    public int top() 
    {
         return st.peek();
    }
    
    public int getMin() 
    {
        return mn.peek();
    }
}

class Rextester{

  public static void main(String args[])
    {
        MinStack minStack = new MinStack();
        minStack.push(-2);
        minStack.push(0);
        minStack.push(-3);
        int param1 = minStack.getMin(); 
        minStack.pop();
        int param2 = minStack.top();   
        int param3 = minStack.getMin(); 
        
    System.out.println(param1);
        System.out.println(param2);
        System.out.println(param3);
    }
}

-3
0
-2

Complexity Analysis for Min Stack Leetcode Solution

Time Complexity

O(1) : O(1) for all operations. As we know stack takes constant time for push, pop, and top. For getMin we have used another stack which makes this function also to work in constant time.

Space Complexity 

O(n) : In worst case all operation is push, hence space complexity is O(n).