Minimum Sideway Jumps LeetCode Solution

Problem Statement

Minimum Sideway Jumps LeetCode Solution – There is a 3 lane road of length n that consists of n + 1 points labeled from 0 to n. A frog starts at point 0 in the second lane and wants to jump to point n. However, there could be obstacles along the way.

You are given an array obstacles of length n + 1 where each obstacles[i] (ranging from 0 to 3) describes an obstacle on the lane obstacles[i] at the point i. If obstacles[i] == 0, there are no obstacles at the point i. There will be at most one obstacle in the 3 lanes at each point.

• For example, if obstacles[2] == 1, then there is an obstacle in lane 1 at point 2.

The frog can only travel from point i to point i + 1 on the same lane if there is not an obstacle on the lane at the point i + 1. To avoid obstacles, the frog can also perform a side jump to jump to another lane (even if they are not adjacent) at the same point if there is no obstacle in the new lane.

• For example, the frog can jump from lane 3 at point 3 to lane 1 at point 3.

Return the minimum number of side jumps the frog needs to reach any lane at point n starting from lane 2 at point 0.

Note: There will be no obstacles on points 0 and n.

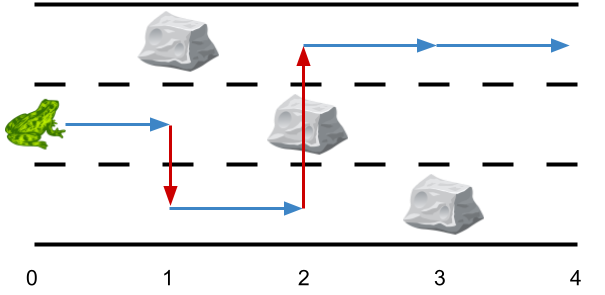
Input: obstacles = [0,1,2,3,0]
Output: 2 
Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps (red arrows).
Note that the frog can jump over obstacles only when making side jumps (as shown at point 2).

Explanation

dp[0] = minimum jump to reach lane 1
dp[1] = minimum jump to reach lane 2
dp[2] = minimum jump to reach lane 3
If meet a stone, set its dp[i] to infinity.
result equals to min(dp)

Code

C++ Code For Minimum Sideway Jumps

class Solution {
public:
    int minSideJumps(vector<int>& A) {
        int dp[] = {1, 0, 1};
        for (int a: A) {
            if (a > 0)
                dp[a - 1] = 1e6;
            for (int i = 0; i < 3; ++i)
                if (a != i + 1)
                    dp[i] = min(dp[i], min(dp[(i + 1) % 3], dp[(i + 2) % 3]) + 1);
        }
        return min(dp[0], min(dp[1], dp[2]));
    }
};

Java Code For Minimum Sideway Jumps

class Solution {
    public int minSideJumps(int[] A) {
        int[] dp = new int[]{1, 0, 1};
        for (int a: A) {
            if (a > 0)
                dp[a - 1] = 1000000;
            for (int i = 0; i < 3; ++i)
                if (a != i + 1)
                    dp[i] = Math.min(dp[i], Math.min(dp[(i + 1) % 3], dp[(i + 2) % 3]) + 1);
        }
        return Math.min(dp[0], Math.min(dp[1], dp[2]));
    }
}

Python Code For Minimum Sideway Jumps

class Solution:
    def minSideJumps(self, A):
        dp = [1, 0, 1]
        for a in A:
            if a:
                dp[a - 1] = float('inf')
            for i in range(3):
                if a != i + 1:
                    dp[i] = min(dp[i], dp[(i + 1) % 3] + 1, dp[(i + 2) % 3] + 1)
        return min(dp)

Complexity Analysis for Minimum Sideway Jumps LeetCode Solution

Time Complexity

O(N)

Space Complexity

O(1)