Minimum Time to Collect All Apples in a Tree LeetCode Solution

Table of Contents

Problem Statement

Minimum Time to Collect All Apples in a Tree LeetCode Solution – Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [a_i, b_i] means that exists an edge connecting the vertices a_i and b_i. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apple.

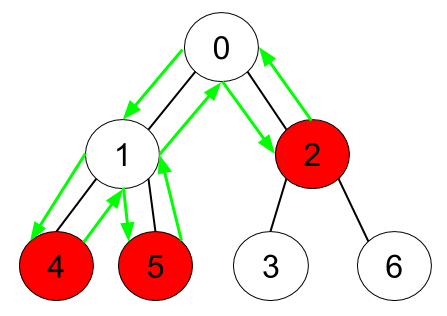
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8 
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.

Explanation

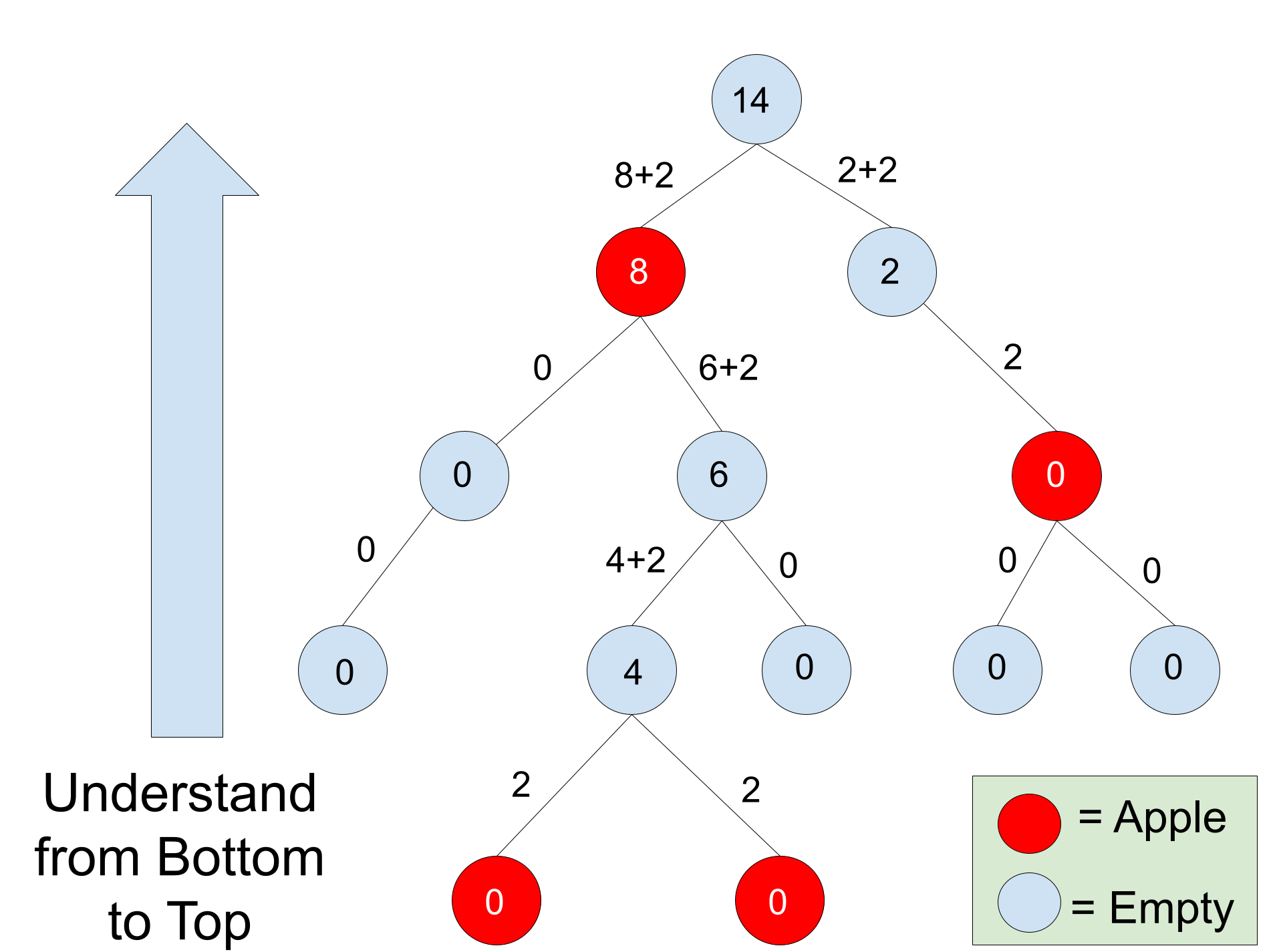
Let’s consider we are at a node, say p, we will collect all apples in p’s subtree before returning back to the original root. This will avoid traveling the same path multiple times.
Say, the root is where we start, p is a node in the tree and p has two children – child1, child2 – and both of them have an apple each.

So the path we need to follow is :

root –> p –> child1 –> p –> child2 –> p —> root

Thus, seeing the above pattern we can infer that it’s a simple DFS traversal but we need to add the cost of traversal two times for any edge e because we also need to come back to it after collecting the apples.

Code

C++ Code for Minimum Time to Collect All Apples in a Tree

class Solution {
public:
    unordered_map<int, vector<int>> g; // to store the graph
    unordered_map<int, bool> visited; // to stop exploring same nodes again and again.
  
    void createGraph(vector<vector<int>>& edges) {
      for (auto e: edges) {
        g[e[0]].push_back(e[1]); // adjecency list representation        
        g[e[1]].push_back(e[0]); // adjecency list representation
      }
    }
  
    int dfs(int node, int myCost, vector<bool>& hasApple) {
    if (visited[node]) {
      return 0;
    }
    visited[node] = true;
    
      int childrenCost = 0; // cost of traversing all children. 
      for (auto x: g[node]) { 
        childrenCost += dfs(x, 2, hasApple);  // check recursively for all apples.
      }

      if (childrenCost == 0 && hasApple[node] == false) {
    // If no child has apples, then we won't traverse the subtree, so cost will be zero.
    // similarly, if current node also does not have the apple, we won't traverse this branch at all, so cost will be zero.
        return 0;
      }
    
    // Children has at least one apple or the current node has an apple, so add those costs.
      return (childrenCost + myCost);
    }
  
    int minTime(int n, vector<vector<int>>& edges, vector<bool>& hasApple) {
      createGraph(edges); // construct the graph first.
      return dfs(0, 0, hasApple); // cost of reaching the root is 0. For all others, its 2.
    }
};

Java Code for Minimum Time to Collect All Apples in a Tree

class Solution {
    public int minTime(int n, int[][] edges, List<Boolean> hasApple) {
        
        Map<Integer, List<Integer>> graph = createGraph(edges); // to store the graph
        Map<Integer, Boolean> visited = new HashMap<>();
    
        return dfs(graph, 0, hasApple, 0, visited); // cost of reaching the root is 0. For all others, its 2.
      
    }
    
    private int dfs(Map<Integer, List<Integer>> graph, int node, List<Boolean> hasApple, int myCost, Map<Integer, Boolean> visited) {
        Boolean v = visited.getOrDefault(node, false);
    if (v) {
      return 0;
    }
    visited.put(node, true);
    
        int childrenCost = 0; // cost of traversing all children. 
      
        for(int n : graph.getOrDefault(node, new ArrayList<>())) {
            childrenCost += dfs(graph, n, hasApple, 2, visited); // check recursively for all apples in subtrees.
        }
      
        if (childrenCost == 0 && hasApple.get(node) == false) {
          // If no child has apples, then we won't traverse the subtree, so cost will be zero.
          // similarly, if current node also does not have the apple, we won't traverse this branch at all, so cost will be zero.
          return 0;
        }
      
        return childrenCost + myCost;
    }
    
    private Map<Integer, List<Integer>> createGraph(int[][] edges) {
        Map<Integer, List<Integer>> graph = new HashMap<>();
      
        for(int i = 0; i < edges.length; i++) {
            List<Integer> list = graph.getOrDefault(edges[i][0], new ArrayList<>()); // Adjecency list representation.
            list.add(edges[i][1]);
            graph.put(edges[i][0], list);
      
      list = graph.getOrDefault(edges[i][1], new ArrayList<>()); // Adjecency list representation.
            list.add(edges[i][0]);
            graph.put(edges[i][1], list);
        }
      
        return graph;
    }
}

Python Code for Minimum Time to Collect All Apples in a Tree

class Solution:
    def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:
      adj = [[] for _ in range(n)]
      for u, v in edges:
          adj[u].append(v)
          adj[v].append(u)
      visited = set()
      def dfs(node):
          if node in visited:
              return 0
          visited.add(node)
          secs = 0
          for child in adj[node]:
              secs += dfs(child)
          if secs > 0:
              return secs + 2
          return 2 if hasApple[node] else 0
      return max(dfs(0) - 2, 0)

Complexity Analysis for Minimum Time to Collect All Apples in a Tree LeetCode Solution

Time Complexity

DFS of a directed graph takes O (V + E) where V and E are the number of Vertices (nodes) and edges.

Space Complexity

We keep a visited array that takes O(V) space.