Minimum Value to Get Positive Step by Step Sum Leetcode Solution

Problem Statement

In this problem, we are given a sequence of numbers (may be positive negative or zero). We have to take a positive integer with us and then we will start adding all integers of this array from left to right with it.
We want the minimum positive integer that we should take in the start, so that, at any time our current sum will always remain positive.

Example

nums = [-3,2,-3,4,2]

5

Explanation:

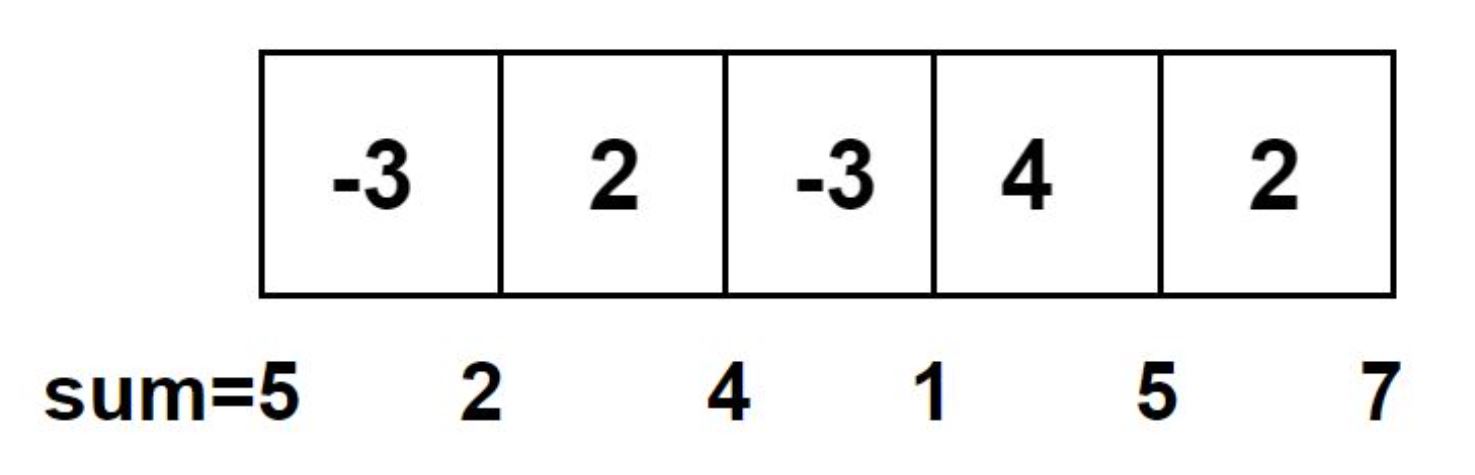
We can see here that if we choose startValue=5, we get all intermediate sum positive. We can check for startValue=4 also, which is not correct solution.

nums = [1,2]

1

Explanation:

Minimum start value should be positive.

Approach

Suppose, we have array , nums = [-3,2,-3,4,2]
Now if we choose initial value as 2, and keep adding elements from left to right, then:

In above example, we have chosen initial value as 2. Our sum will not remain positive every time, so we need some larger element.

Let the initial val be 5.

Now, we can clearly see that if starting value is 5 then, we can surely travel throughout the array keeping our current sum positive always. 5 can be the answer if it is the smallest integer doing so.
Let’s think of a situation if we choose val=0 with us at the start.

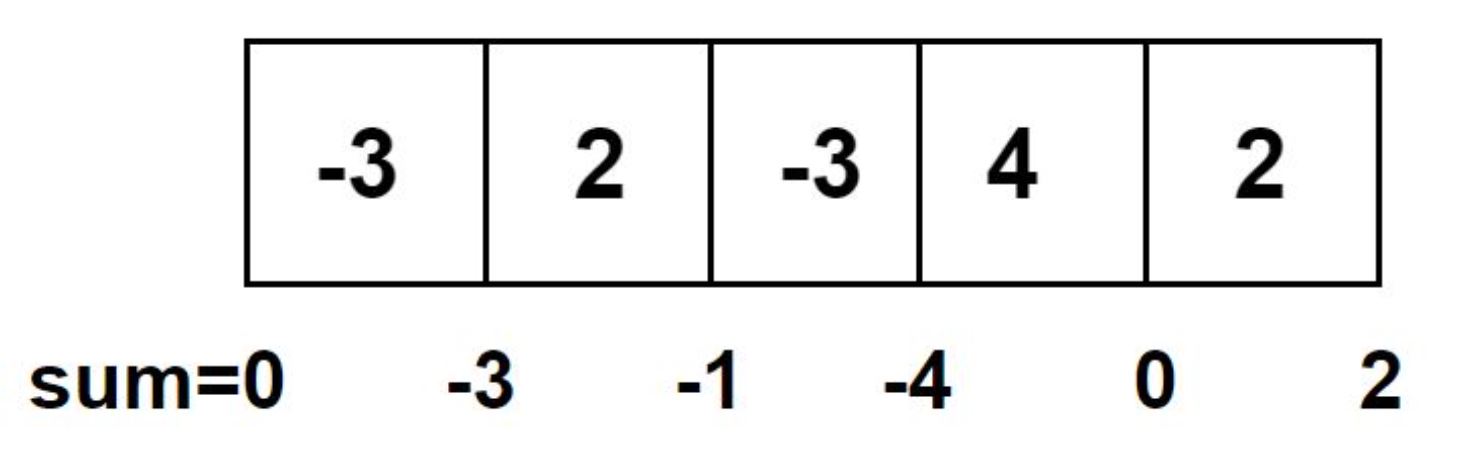
Now, can we say that if we overcome the value of most negative current sum (-4 in current example), then we can clearly pass the array without any problem.
Like, in above example, the most negative value is -4, To overcome it, we have to make it 1 (because, smallest positive integer needed).

So we want value 1-(-4)=5 to pass the most negative situation.
we have also seen that 5 can pass the solution.

And if there is no negative current sum, we will just output 1 because we want a positive integral solution.

So, our algorithm will be :

1. We have to search for most negative solution, so we will traverse the whole array.
2. In each iteration of the loop we will check if current sum is minimum or not and we will update our min value accordingly.
3. Finally to make this most negative value to 1, we will just subtract it from 1. (e.g. if min = -4, val=1-(-4)=5).

Implementation

C++ Program for Minimum Value to Get Positive Step by Step Sum Leetcode Solution

#include <iostream>
#include<vector>
using namespace std;

int minStartValue(vector<int>& nums) {
    
    int min=0,sum=0;
    for (int i = 0; i < nums.size(); i++){
        sum+=nums[i];
        min=min<sum?min:sum;
    }
    
    return 1-min;
}

int main() {
    vector<int> nums{-3,2,-3,4,2}; 
    cout<<minStartValue(nums)<<endl;	
  return 0;
}

5

Java Program for Minimum Value to Get Positive Step by Step Sum Leetcode Solution

import java.util.*;

class Rextester{
    
    public static int minStartValue(int[] nums) 
    {
        Integer min=0,sum=0;
        for(int i:nums){
            sum+=i;
            min=Math.min(min,sum);
        }
        return 1-min;
    }
    
    public static void main(String args[])
    {
       	int[]nums={-3,2,-3,4,2};
        int ans=minStartValue(nums);
        System.out.println(ans);
    }
}

5

Complexity Analysis for Minimum Value to Get Positive Step by Step Sum Leetcode Solution

Time Complexity

O(n): Because, we are traversing the given array linearly, thus our time complexity will be O(n).

Space Complexity 

O(1): We haven’t used any extra space, thus our space complexity will be constant.