Number of Dice Rolls With Target Sum LeetCode Solution

Problem Statement

Number of Dice Rolls With Target Sum LeetCode Solution – You have n dice and each die has k faces numbered from 1 to k.

Given three integers n, k, and target, return the number of possible ways (out of the kⁿ total ways) to roll the dice so the sum of the face-up numbers equals target. Since the answer may be too large, return it modulo 10⁹ + 7.

Input: n = 1, k = 6, target = 3
Output: 1
Explanation: You throw one die with 6 faces.
There is only one way to get a sum of 3.

Explanation

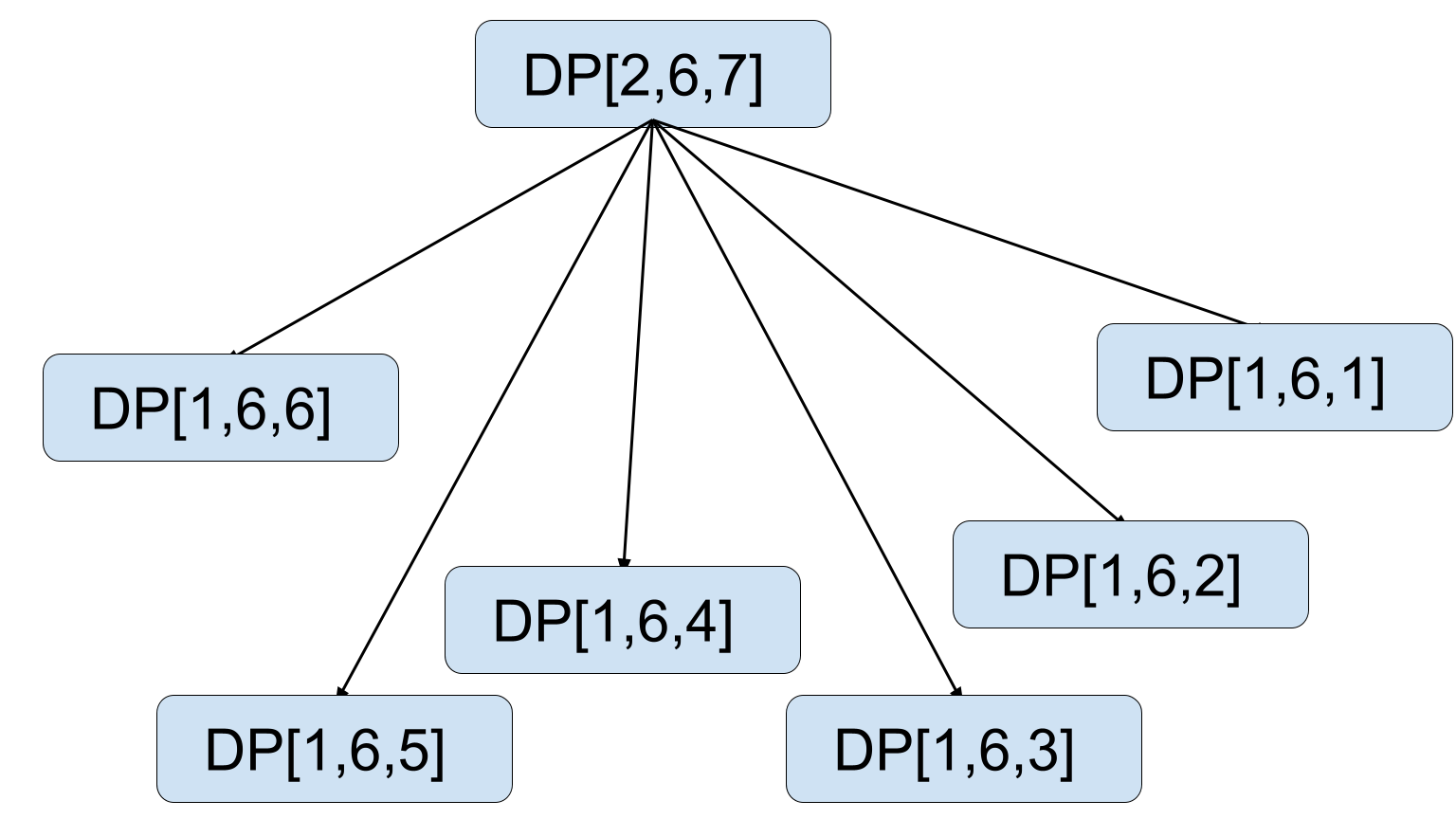
As an initial example, pretend we have 5 dice with 6 faces each and we want to determine how many ways to make 18.

In other words, what is dp(5, 6, 18)?

At first glance, this seems difficult and overwhelming. But if we make one simple observation, we can reduce this big problem into several smaller sub-problems. We have 5 dice, but let’s first just look at ONE of these dice (say the last one). This die can take on f=6 different values (1 to 6), so we consider what happens when we fix its value to each possibility (6 cases):

Case 1: The last die is a 1. The remaining 4 dice must sum to 18-1=17. This can happen dp(4, 6, 17) ways.
Case 2: The last die is a 2. The remaining 4 dice must sum to 18-2=16. This can happen dp(4, 6, 16) ways.
Case 3: The last die is a 3. The remaining 4 dice must sum to 18-3=15. This can happen dp(4, 6, 15) ways.
Case 4: The last die is a 4. The remaining 4 dice must sum to 18-4=14. This can happen dp(4, 6, 14) ways.
Case 5: The last die is a 5. The remaining 4 dice must sum to 18-5=13. This can happen dp(4, 6, 13) ways.
Case 6: The last die is a 6. The remaining 4 dice must sum to 18-6=12. This can happen dp(4, 6, 12) ways.

dp(5, 6, 18) = dp(4, 6, 17) + dp(4, 6, 16) + dp(4, 6, 15) + dp(4, 6, 14) + dp(4, 6, 13) + dp(4, 6, 12)

We sum up the solutions in these 6 cases to arrive at our result. Of course, each of these cases branches off into 6 cases of its own, and the recursion only resolves when d=0. The handling of this base case is explained below.
The general relation is:

dp(d, f, target) = dp(d-1, f, target-1) + dp(d-1, f, target-2) + … + dp(d-1, f, target-f)

The base case occurs when d = 0. We can make target=0 with 0 dice, but nothing else.
So dp(0, f, t) = 0 iff t != 0, and dp(0, f, 0) = 1.

Use memoization to avoid repeated calculations and don’t consider negative targets.

Code

C++ Code for Number of Dice Rolls With Target Sum

class Solution {
public:
    int numRollsToTarget(int d, int f, int target) {
        int m=1000000007;
        vector<vector<int> > dp(d+1, vector<int>(target+1, 0));
        dp[0][0]=1;
        for(int i=1; i<=d; i++){
            for(int j=1; j<=target; j++){
                for(int k=1; k<=f; k++){
                    if(k<=j)
                        dp[i][j]=((dp[i][j]%m)+(dp[i-1][j-k]%m))%m;
                }
            }
        }
        return dp[d][target];
    }
};

Java Code for Number of Dice Rolls With Target Sum

class Solution {
    public int numRollsToTarget(int n, int k, int target) {
        int[][] dp=new int[n+1][target+1];
        dp[0][0]=1;
        int m=1000000007;
        for(int i=1;i<=n;i++) {
            for(int j=1;j<=target;j++) {
                for(int face=1;face<=k;face++) {
                    if ((j-face)<0 ) continue;
                    dp[i][j]=(dp[i][j]%m+(dp[i-1][j-face])%m)%m;
                }
                
            }
        }
        return dp[n][target];    
        }
}

Python Code for Number of Dice Rolls With Target Sum

class Solution:
    def numRollsToTarget(self, d: int, f: int, target: int) -> int:
        memo = {}
        def dp(d, target):
            if d == 0:
                return 0 if target > 0 else 1
            if (d, target) in memo:
                return memo[(d, target)]
            to_return = 0
            for k in range(max(0, target-f), target):
                to_return += dp(d-1, k)
            memo[(d, target)] = to_return
            return to_return
        return dp(d, target) % (10**9 + 7)

Complexity Analysis for Number of Dice Rolls With Target Sum LeetCode Solution

Time Complexity

O(d * target * faces)

Space Complexity

O(d * target)